If you know two angle measures and a side length on a triangle, you can use the Law of Sines to find the missing parts of the triangle. In this case, you need to know either two angles and the side in between them (angle-side-angle, or ASA), or two angles and a consecutive side (angle-angle-side, or AAS).
Whenever you're given two angles, you can find the third one immediately and work from there. In both of these cases, you can find exactly one solution for the triangle in question.
Solve a Triangle Using ASA
An ASA triangle means that you're given two angles and the side between them in a problem. For example, a problem could state that
as shown in the figure. You also could be given
This figure has all the given and unknown parts labeled for you.
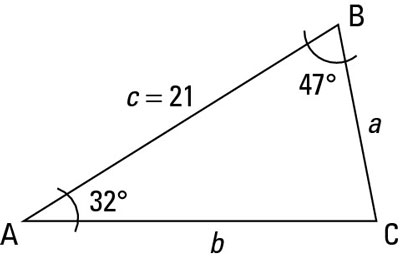
To find the missing information with the Law of Sines, follow these steps:
Determine the measure of the third angle.
As a rule,

So by plugging in what you know about the angles in this problem, you can solve for the missing angle:

Set up the Law of Sines formula, filling in what you know.
Given that the formula for the Law of Sines looks like this:

the formula here sets up like this:

Set one fraction with an unknown numerator and the fraction with a known numerator equal to each other and cross multiply.
If you use, say, the first and third fractions, the equation look like this:

Cross multiplying, you have

Find the decimal approximation of the missing side using your calculator.
Because sin 101 degrees is just a number, you can divide both sides of the equation by it to isolate the variable:

Repeat Steps 3 and 4 to solve for the other missing side.
Setting the second and third fractions equal to each other, you have this equation:

This equation becomes

when you cross multiply. Isolate the variable and solve for it:

State all the parts of the triangle as your final answer.
Some answers may be approximate, so make sure you maintain the proper signs:

Solve a Triangle Using AAS
In many trig problems, you're given two angles and a side that isn't between them. This type of problem is called an AAS problem. For example, you may be given
as shown in this figure.
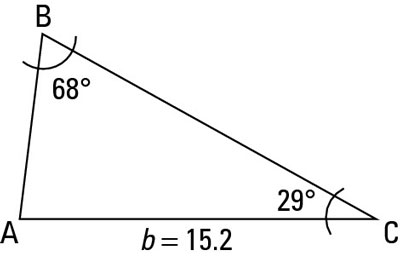
Notice that if you start at side b and move counterclockwise around the triangle, you come to
This check is a good way to verify whether a triangle is an example of AAS.
After you find the third angle, an AAS problem just becomes a special case of ASA. Here are the steps to solve:
Determine the measure of the third angle.
You can say that

Set up the Law of Sines formula, filling in what you know.

Set one fraction with an unknown numerator and the fraction with a known numerator equal to each other and then cross multiply.
Say that you choose to use a and b:

Cross multiplying, you have

Solve for the missing side.
You divide by sin 68 degrees, so

Repeat Steps 3 and 4 to solve for the other missing side.
Setting b and c equal to each other, you have this equation:

Cross multiply:

Divide by sin 68 degrees to isolate the variable and solve:

State all the parts of the triangle as your final answer.
Your final answer sets up as follows:







