Periodicity identities illustrate how shifting the graph of a trig function by one period to the left or right results in the same function. The functions of sine, cosine, secant, and cosecant repeat every 2(pi) units; tangent and cotangent, on the other hand, repeat every pi units.
The following identities show how the different trig functions repeat:
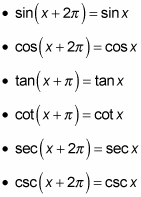
You can use periodicity identities to simplify expressions. Similar to the co-function identities, you use the periodicity identities when you see
inside a trig function. Because adding (or subtracting) 2(pi) radians from an angle gives you a new angle in the same position, you can use that idea to form an identity. For tangent and cotangent only, adding or subtracting pi radians from the angle gives you the same result, because the period of the tangent and cotangent functions is pi.
For example, to simplify
follow these steps:
Replace all trig functions with 2(pi) — or pi in the case of the cotangent — inside the parentheses with the appropriate periodicity identity.
For this example,

Simplify the new expression.

To find a common denominator to add the fractions, multiply the first term by

Here's the new fraction:

Add them together to get this:

You can see a Pythagorean identity in the numerator, so replace

with 1. Therefore, the fraction becomes







