If you take the graph of y = sin x and shift it to the left by pi/2 units, it looks exactly like the graph of y = cos x. The same is true for tangent and cotangent, as well as secant and cosecant. That's the basic premise of co-function identities — they say that the sine and cosine functions take on the same values, but those values are shifted slightly on the coordinate plane when you look at one function compared to the other.
Here is a list of co-function identities:
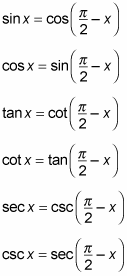
The co-function identities are great to use whenever you see pi/2 inside the grouping parentheses. You may see functions in the expressions such as
If the quantity inside the trig function looks like
you'll know to use the co-function identities.
For example, to simplify
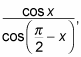
follow these steps:
Look for co-function identities and substitute.
First realize that cos(pi/2 – x) is the same as sin x because of the co-function identity. That means you can substitute sin x in for cos(pi/2 – x) to get

Look for other substitutions you can make.
Because of the reciprocal identity for cotangent,

is the same as cot x.






