Infinite square wells, in which the walls go to infinity, are a favorite in quantum physics problems. In some instances, you may want to shift things so that the square well is symmetric around the origin.
For example, the standard infinite square well looks like this:
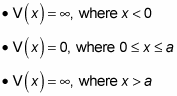
But what if you want to move the square well so that it extends from
Here's what the new infinite square well looks like in this case:
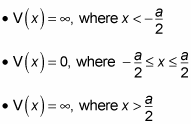
You can translate from this new square well to the old one by adding a/2 to x, which means that you can write the wave function for the new square well in this equation as follows:
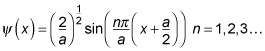
Doing a little trig gives you the following equations:
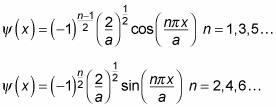
So as you can see, the result is a mix of sines and cosines. The bound states are these, in increasing quantum order:
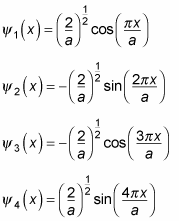
And so on.
Note that the cosines are symmetric around the origin:
The sines are anti-symmetric:






