Quantum physics experiments take place in the lab frame, but you do scattering calculations in the center-of-mass frame, so you have to know how to relate the angle between the two frames.
Here's how this works: The following figure shows scattering in the lab frame.
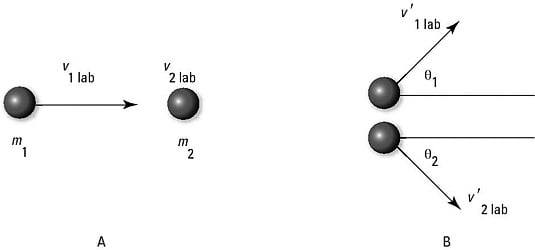
One particle, traveling at
is incident on another particle that's at rest
and hits it. After the collision, the first particle is scattered at
and the other particle is scattered at
Now in the center-of-mass frame, the center of mass is stationary and the particles head toward each other. After they collide, they head away from each other at angles
You have to move back and forth between these two frames — the lab frame and the center-of-mass frame — so you need to relate the velocities and angles (in a nonrelativistic way).
To relate the angles
you start by noting that you can connect
using the velocity of the center of mass,
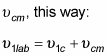
In addition, here's what you can say about the velocity of particle 1 after it collides with particle 2:
Now you can find the components of these velocities:
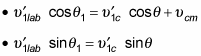
Dividing the equation in the second bullet by the one in the first gives you
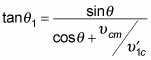
But wouldn't it be easier if you could relate
by something that didn't involve the velocities, only the masses, such as the following?
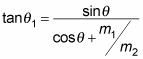
Well, you can. To see that, start with
And you can show that
You can also use the conservation of momentum to say what happens after the collision. In fact, because the center of mass is stationary in the center-of-mass frame, the total momentum before and after the collision is zero in that frame, like this:
Therefore
And after the collision,
which means that
Also, if the collision is elastic, kinetic energy is conserved in addition to momentum, so that means the following is true:
Substituting
into this equation gives you
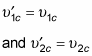
Given these two equations, you can redo
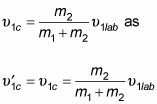
Dividing the magnitude of each side of
by the magnitude of the above equation gives you
And because you saw earlier that
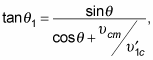
substituting
into this equation gives you at last
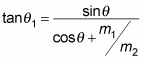
Okay, that relates
which is what you were trying to do. Using the relation
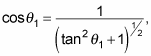
you can rewrite
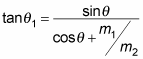
as the following:
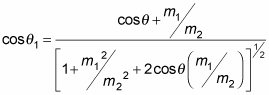
You can also relate
You can show that
which, using a little trig, means that
You've now related the angles between the lab and center-of-mass frames.

