You can use the following six methods to prove that a quadrilateral is a rhombus. The last three methods in this list require that you first show (or be given) that the quadrilateral in question is a parallelogram:
If all sides of a quadrilateral are congruent, then it’s a rhombus (reverse of the definition).
If the diagonals of a quadrilateral bisect all the angles, then it’s a rhombus (converse of a property).
If the diagonals of a quadrilateral are perpendicular bisectors of each other, then it’s a rhombus (converse of a property).
Tip: To visualize this one, take two pens or pencils of different lengths and make them cross each other at right angles and at their midpoints. Their four ends must form a diamond shape — a rhombus.
If two consecutive sides of a parallelogram are congruent, then it’s a rhombus (neither the reverse of the definition nor the converse of a property).
If either diagonal of a parallelogram bisects two angles, then it’s a rhombus (neither the reverse of the definition nor the converse of a property).
If the diagonals of a parallelogram are perpendicular, then it’s a rhombus (neither the reverse of the definition nor the converse of a property).
Here’s a rhombus proof for you. Try to come up with a game plan before reading the two-column proof.

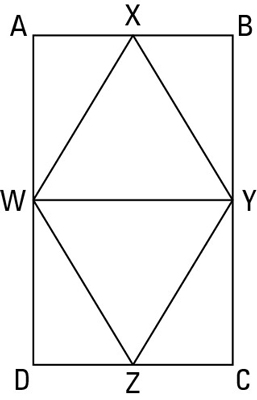
Statement 1:
Reason for statement 1: Given.
Statement 2:
Reason for statement 2: Opposite sides of a rectangle are congruent.
Statement 3:

Reason for statement 3: Given.
Statement 4:
Reason for statement 4: Like Divisions Theorem.
Statement 5:
Reason for statement 5: All angles of a rectangle are right angles.
Statement 6:
Reason for statement 6: All right angles are congruent.
Statement 7:
Reason for statement 7: Given.
Statement 8:
Reason for statement 8: A midpoint divides a segment into two congruent segments.
Statement 9:
Reason for statement 9: SAS, or Side-Angle-Side (4, 6, 8)
Statement 10:
Reason for statement 10: CPCTC (Corresponding Parts of Congruent Triangles are Congruent).
Statement 11:

Reason for statement 11: Given.
Statement 12:
Reason for statement 12: If a triangle is isosceles, then its two legs are congruent.
Statement 13:
Reason for statement 13: Transitivity (10 and 12).
Statement 14:
Reason for statement 14: If a quadrilateral has four congruent sides, then it’s a rhombus.

