When a square root appears inside a trigonometric identity, and you know both sides are equal, you have to square both sides at some point to finish the proof. However, if you don't know both sides are equal, you have to start with one side and attempt to get it equal to the other side. For example, say you have to prove
The square root on the right means that you should start on that side:
Look for identities.
You can see a double angle:
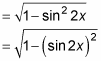
That gives you

which is the same as

Change all sines to cosines or vice versa.
Because you have more sines, change the cos2 x by using the Pythagorean identity to get this equation:

Distribute the equation.
You end up with

Using the commutative and associative properties of equality, you get

which proves that the right side equals the left side.






