By adding a capacitor to an operational-amplifier (op amp) circuit, you can use the op amp circuit to do more-complex mathematical operations, like integration and differentiation. Practically speaking, you use capacitors instead of inductors because inductors are usually bulkier than capacitors.
Create an op amp integrator
Here is an op amp circuit that has a feedback element as a capacitor. The circuit is configured similarly to an inverting amplifier.
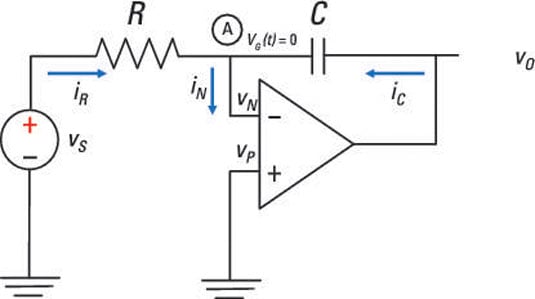
The cool thing about this op amp circuit is that it performs integration. The circuit electronically calculates the integral of any input voltage, which is a lot simpler (and less painful!) than banging your head on the table as you try to integrate a weird function by hand.
Watch and learn how this circuit performs this incredible feat called integration. First, you use a KCL equation at Node A:
iR(t) + iC(t) = iN(t)
Ohm’s law (i = v/R) gives you the current through the resistor:
You get the current through the capacitor using the i-v relationship of a capacitor:
For ideal op amp devices, the circuit gives you vG(t) = 0 (virtual ground) and iN = 0 (infinite input resistance). Substituting these op amp constraints for iR(t) and iC(t) into the KCL equation gives you
Then integrate both sides of the preceding equation. You wind up with the following output voltage vo(t):
The initial output voltage vo(0) across the capacitor — that, is the voltage at t = 0 — is 0. If vo(0) = 0, then the output-voltage equation reduces to
The op amp circuit accepts an input voltage and gives you an inverted output that’s proportional to the integral of the input voltage.
Derive an op amp differentiator
With op amp circuits where the resistor is the feedback element and the capacitor is the input device (like the one shown here), you can perform differentiation electronically.
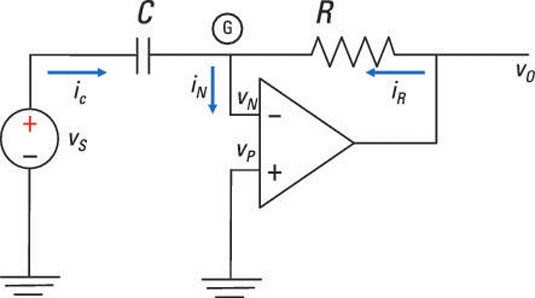
You follow the same process as the one you use to find the relationship for an op amp integrator. Begin with a KCL equation at Node G:
iR(t) + iC(t) = iN(t)
The current through the resistor is given by Ohm’s law (i = v/R):
The current through the capacitors is given by the i-v relationship of a capacitor:
For ideal op amp devices, the circuit gives you vG = 0 (virtual ground) and iN = 0 (infinite input resistance). Substituting these op amp constraints for iR(t) and iC(t) into the KCL equation gives you the following:
Solving for vo, you wind up with the following output voltage vo(t):
So if you are given an input voltage, you won’t even raise a sweat in getting its derivative as an output. The inverted output is simply proportional to the derivative of the input voltage.

