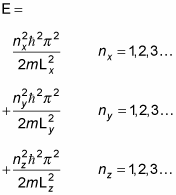In your quantum physics course, you may be asked to normalize the wave function in a box potential. Here's an example: consider the wave function
In the x dimension, you have this for the wave equation:
So the wave function is a sine wave, going to zero at x = 0 and x = Lz. You can also insist that the wave function be normalized, like this:
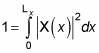
By normalizing the wave function, you can solve for the unknown constant A. Substituting for X(x) in the equation gives you the following:

Therefore,
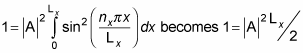
which means you can solve for A:
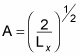
Great, now you have the constant A, so you can get X(x):
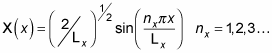
Now get
You can divide the wave function into three parts:
By analogy with X(x), you can find Y(y) and Z(z):
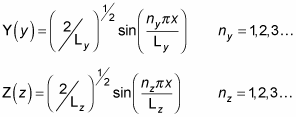
So
equals the following:
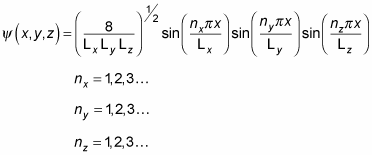
That's a pretty long wave function. In fact, when you're dealing with a box potential, the energy looks like this: