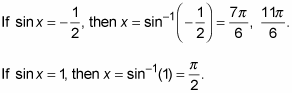The technique of multiplying through a trigonometry equation by a carefully selected function shouldn’t be your first choice — or your second, third, or fourth choice. This method is usually a last resort. Not that the method is terribly hard; it just requires sitting back and looking at the equation, and magically coming up with the best function to use in the multiplication.
You can find the best function by guess or by golly, but then, that would take all the fun out of it — you want to guess right the first time. Here’s an example of an equation on which this technique works well.
Solve 2sin x – csc x = 1 for all the solutions between 0 and 2π.
Multiply each term by sin x.
Why sin x? This function is chosen because you can see that the products of the individual terms would be either different powers of sine or just a number. Notice that the product of the term csc x and its reciprocal, sin x, is 1.
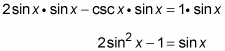
Subtract sin x from each side to set the equation equal to 0.
2sin2 x – sin x – 1 = 0
Factor the quadratic equation.
(2sin x + 1)(sin x – 1) = 0
Set each factor equal to 0.

Solve for the values that satisfy the equations.