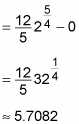Sometimes if you want to measure the volume of an object, you need to turn it on its side so that you can use the meat-slicer method. This method works best with solids that have similar cross sections.
Here’s the plan:
Find an expression that represents the area of a random cross section of the solid in terms of x.
Use this expression to build a definite integral (in terms of dx) that represents the volume of the solid.
Evaluate this integral.
 Using inverses to get a problem ready for the meat-slicer method.
Using inverses to get a problem ready for the meat-slicer method.
For example, suppose that you want to measure the volume of the solid shown here. The base of this solid (light gray) is bounded on its sides by the function y = x4 between the x-axis at the bottom and y = 2 across the top. The figure is 3 units high, such that the cross section when you slice parallel with the x-axis is a series of isosceles triangles, each with a height of 3 and a base that’s the width across the function y = x4.
The good news is that this solid has cross sections that are all similar triangles, so the meat-slicer method will work. Unfortunately, as the problem currently stands, you’d have to make your slices perpendicular to the y-axis. But to use the meat-slicer method, you must make your slices perpendicular to the x-axis.
To solve the problem, you first need to flip the solid over to the x-axis, as shown on the right side of the figure. The easiest way to do this is to use the inverse of the function y = x4. To find the inverse, switch x and y in the equation and solve for y:
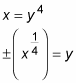
Note that the resulting equation
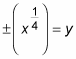
in this case isn’t a function of x because a single x-value can produce more than one y-value. However, you can use this equation in conjunction with the meat-slicer method to find the volume that you’re looking for.
Find an expression that represents the area of a random cross section of the solid.
The cross section is an isosceles triangle with a height of 3 and a base of
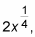
so use the formula for the area of a triangle:
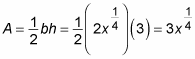
Use this expression to build a definite integral that represents the volume of the solid.
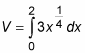
Solve the integral.
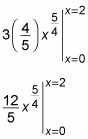
Now evaluate this expression: