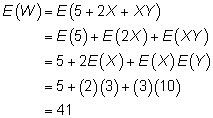In econometrics, the expected value (or mean) of a random variable provides a measure of central tendency, which means that it provides one measurement of where the data tends to cluster.
The expected value is the average of a random variable. If you have a discrete random variable, you can calculate the expected value with the equation
where X represents the different possible values for the random variable, and f(X) is the probability that each value will occur.
If you have a continuous random variable, then you calculate the expected value with this equation:
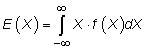
Although you may need to recognize the difference between discrete and continuous random variables, you probably won’t need to perform manual calculations of expected value for continuous random variables. You should, however, know how to perform manual calculations for a discrete random variable.
Suppose you're examining random variable X with the probability distribution shown in the first two columns of the table. You can find the expected value by multiplying each possible value for X by its probability of occurring and then adding those values. You show this operation in the third column, which gives you E(X) = 1.5.
| X | Probability (f(X)) | X * f(X) |
|---|---|---|
| 0 | 0.125 | 0 |
| 1 | 0.375 | 0.375 |
| 2 | 0.375 | 0.750 |
| 3 | 0.125 | 0.375 |
| Total: | 1 | 1.5 |
If you’re manipulating equations containing an expected value operator, you’ll find the following five properties useful:
The expected value of a constant is just the constant itself: E(a) = a
The expected value of two random variables added together is equal to the sum of each of their expected values: E(X + Y) = E(X) + E(Y)
The expected value of a random variable multiplied by a constant is equal to the constant multiplied by the expected value of the random variable: E(aX) = aE(X)
If X and Y are independent random variables, then the expected value of their product is equal to the product of their expected values: E(XY) = E(X)E(Y)
If X and Y are independent random variables, then the expected value of their ratio is equal to the ratio of their expected values:
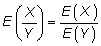
Suppose you create a random variable W defined by W = 5 + 2X + XY, where the random variable X has an expected value equal to 3, the random variable Y has an expected value equal to 10, and they’re independent random variables. Using the expected-value properties, you calculate the expected value of W as