How to Locate the Center of a Circle

You can use algebra to find the center of a circle. If the endpoints of one diameter of a circle are (x₁,y₁) and (x₂,y₂), then the center of the circle has the following coordinates:

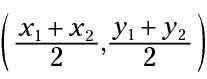
You probably noticed that the center of a circle is the same as the diameter’s midpoint. The center of the circle separates the diameter into two equal segments called radii (plural for radius).

The center of a circle is also the midpoint of one of its diameters.

The preceding figure shows a circle with a diameter whose endpoints are (7,4) and (–1,–2). The center of the circle is at (3,1). You get the coordinates for the center by using the formula for the midpoint of a segment:

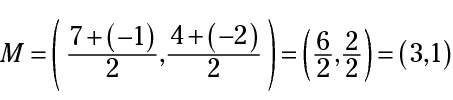
You find the length of the diameter by using the distance formula:

the endpoints of the segment being measured.

For the circle shown in the preceding figure, the diameter is 10 units long.

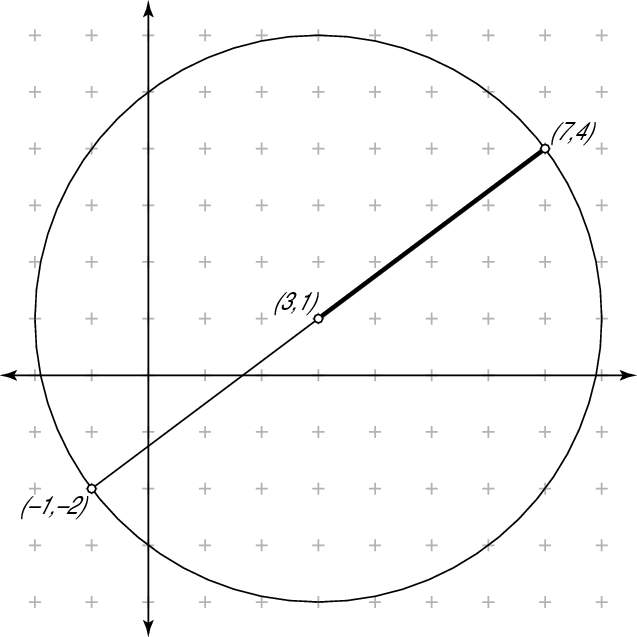
Now here’s how to find the length of one of the radii. Either will do — they’re the same length. In this example, you can figure the radius length from the center of the circle (3,1) to the endpoint of the diameter (7,4):

The radius is 5 units long. But, of course, you expected this answer, because by definition, the radius is half the length of the diameter.