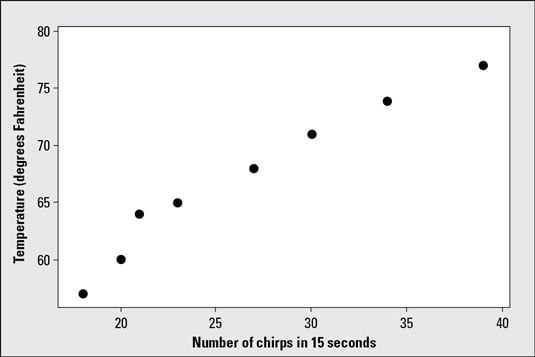
| Temperature Data and Cricket Chirps (Excerpt) | |
| Temperature (Fahrenheit) | Number of Chirps (in 15 Seconds) |
|---|---|
| 57 | 18 |
| 60 | 20 |
| 64 | 21 |
| 65 | 23 |
| 68 | 27 |
| 71 | 30 |
| 74 | 34 |
| 77 | 39 |
You interpret a scatterplot by looking for trends in the data as you go from left to right:
-
If the data show an uphill pattern as you move from left to right, this indicates a positive relationship between X and Y. As the X-values increase (move right), the Y-values tend to increase (move up).
-
If the data show a downhill pattern as you move from left to right, this indicates a negative relationship between X and Y. As the X-values increase (move right) the Y-values tend to decrease (move down).
-
If the data don’t seem to resemble any kind of pattern (even a vague one), then no relationship exists between X and Y.
A linear relationship between X and Y exists when the pattern of X- and Y-values resembles a line, either uphill (with a positive slope) or downhill (with a negative slope).
Scatterplots show possible associations or relationships between two variables. However, just because your graph or chart shows something is going on, it doesn’t mean that a cause-and-effect relationship exists.
For example, a doctor observes that people who take vitamin C each day seem to have fewer colds. Does this mean vitamin C prevents colds? Not necessarily. It could be that people who are more health conscious take vitamin C each day, but they also eat healthier, are not overweight, exercise every day, and wash their hands more often.If this doctor really wants to know if it’s the vitamin C that’s doing it, they need a well-designed experiment that rules out these other factors.

