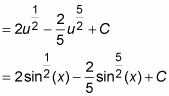When you integrate a trig integral that includes cosine, and if the power of cosine is odd and positive, you can convert and then use substitution to integrate. To make this conversion, you need to know the Pythagorean identity.
Here’s how you integrate a trig integral that contains sines and cosines where the power of cosine is odd and positive. You lop off one cosine factor and put it to the right of the rest of the expression, convert the remaining (even) cosine factors to sines with the Pythagorean identity, and then integrate with the substitution method where u = sin(x). Recall your trusty ol’ Pythagorean identity:
For any angle x,
And thus,
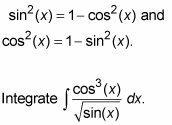
Lop off one cosine factor and move it to the right.
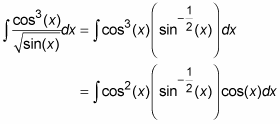
Convert the remaining (even) cosines to sines with the Pythagorean identity and simplify.
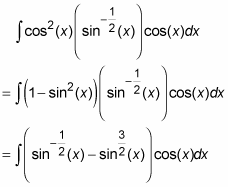
Integrate with substitution, where u = sin(x).
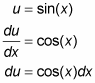
Now substitute
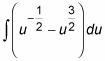
and finish integrating: