You can integrate odd powers of tangents with secants. To integrate tanm x secn x when m is odd — for example, tan7 x sec9 x — you would follow these steps:
Peel off a tan x and a sec x and place them next to the dx:
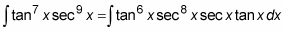
Use the trig identity tan2x = sec2x – 1 to express the remaining tangent factors in terms of secants:
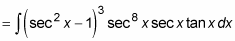
Use the variable substitution u = sec x and du = sec x tan x dx:
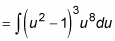
At this point, the integral is a polynomial, and you can evaluate it.

