Sometimes you need to integrate the product of a function (x) and a composition of functions (for example, the function 3x2 + 7 nested inside a square root function). If you were differentiating, you could use a combination of the Product Rule and the Chain Rule, but these options aren’t available for integration.
Given
here’s how you integrate, step by step, using variable substitution:
Declare a variable u as follows and substitute it into the integral:
Here, you assign a value to u: let u = 3x2 + 7. Now substitute u into the integral:
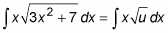
Make one more small rearrangement to place all the remaining x terms together:
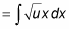
This rearrangement makes clear that you still have to find a substitution for x dx.
Now differentiate the function u = 3x2 + 7:
This gives you the differential,
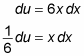
Substitute du/6 for x dx:
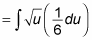
You can move the fraction 1/6 outside the integral:
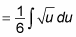
Now you have an integral that you know how to evaluate.
This example puts the square root in exponential form, to make sure that you see how to do this:
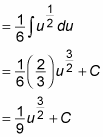
To finish up, substitute 3x2 + 7 for u:
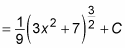
You can now check your integration by differentiating the result:
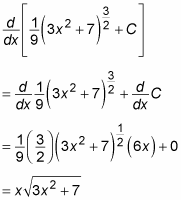
As if by magic, the derivative brings you back to the function you started with.

