If a function is even, the graph is symmetrical about the y-axis. If the function is odd, the graph is symmetrical about the origin.
-
Even function: The mathematical definition of an even function is f(–x) = f(x) for any value of x. The simplest example of this is f(x) = x2 because f(x)=f(-x) for all x. For example, f(3) = 9, and f(–3) = 9. Basically, the opposite input yields the same output.
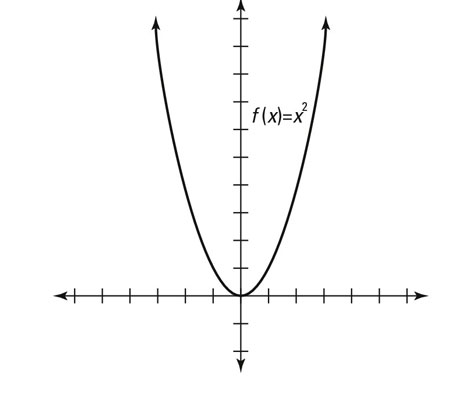 Visually speaking, the graph is a mirror image about the y-axis, as shown here.
Visually speaking, the graph is a mirror image about the y-axis, as shown here. -
Odd function: The definition of an odd function is f(–x) = –f(x) for any value of x. The opposite input gives the opposite output. These graphs have 180-degree symmetry about the origin. If you turn the graph upside down, it looks the same.

The example shown above, f(x) = x3, is an odd function because f(-x)=-f(x) for all x. For example, f(3) = 27 and f(–3) = –27.






