The graph of a quadratic function is a smooth, U-shaped curve that opens either upward or downward, depending on the sign of the coefficient of the x2 term. The vertex and intercepts offer the quickest, easiest points to help with the graph of the parabola.
You can resort to solving for other points if the graph has no x-intercepts or if you need additional information to determine more about the shape.
Another aid to use when graphing parabolas is the axis of symmetry; a parabola is symmetric about a vertical line that runs through the vertex. Points on either side of the axis of symmetry that have the same y-value are equal distances from the axis. The equation of the axis of symmetry is x = h, where (h, k) is the vertex of the parabola.
Sample question
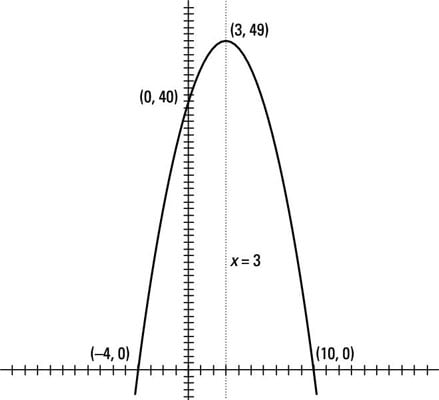
Sketch the graph of the parabola f(x) = –x2 + 6x + 40, labeling any intercepts and the vertex and showing the axis of symmetry.
As you can see, the y-intercept is (0, 40); you can find it by letting all the x’s equal 0 and simplifying. Find the x-intercepts by setting –x2 + 6x + 40 equal to 0 and factoring: 0 = –(x2 – 6x – 40) = –(x + 4)(x – 10); x = –4 and 10, so the intercepts are at (–4, 0) and (10, 0).
The vertex is at (3, 49): You find the x-value and then replace the x’s with 3s and simplify for the y-coordinate.
Practice questions
Sketch the graph of the parabola f(x) = 4x2, labeling any intercepts and the vertex and showing the axis of symmetry.
Sketch the graph of the parabola
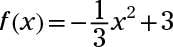
labeling any intercepts and the vertex and showing the axis of symmetry.
Sketch the graph of the parabola f(x) = 3x2 – 6x – 9, labeling any intercepts and the vertex and showing the axis of symmetry.
Sketch the graph of the parabola f(x) = –2x2 + 10x – 8, labeling any intercepts and the vertex and showing the axis of symmetry.
Following are answers to the practice questions:
Sketch the graph of the parabola f(x) = 4x2, labeling any intercepts and the vertex and showing the axis of symmetry.
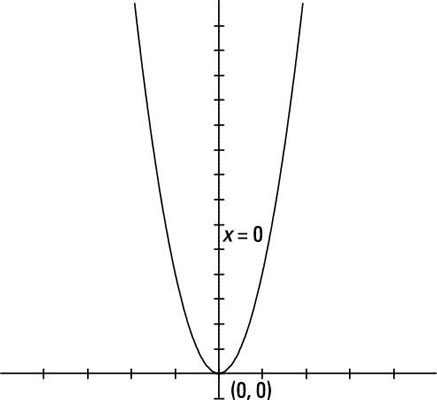
The only intercept is at (0, 0). The parabola opens upward, because 4 is positive. The vertex is at (0, 0), and the equation of the axis of symmetry is x = 0 (which is the y-axis).
Sketch the graph of the parabola
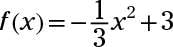
labeling any intercepts and the vertex and showing the axis of symmetry.
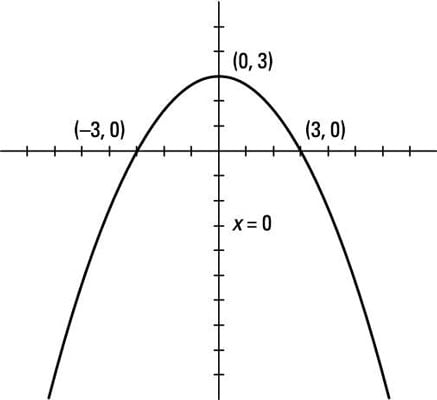
The intercepts are at (0, 3), (3, 0), and (–3, 0). The parabola opens downward, because the coefficient of x2 is negative. The vertex is at (0, 3), the y-intercept, and the equation of the axis of symmetry is x = 0.
Sketch the graph of the parabola f(x) = 3x2 – 6x – 9, labeling any intercepts and the vertex and showing the axis of symmetry.
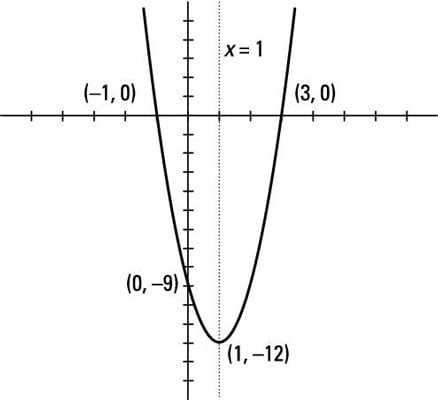
The intercepts are at (0, –9), (3, 0), and (–1, 0). The parabola opens upward, because 3 is positive. The vertex is at (1, –12), and the equation of the axis of symmetry is x = 1.
Sketch the graph of the parabola f(x) = –2x2 + 10x – 8, labeling any intercepts and the vertex and showing the axis of symmetry.
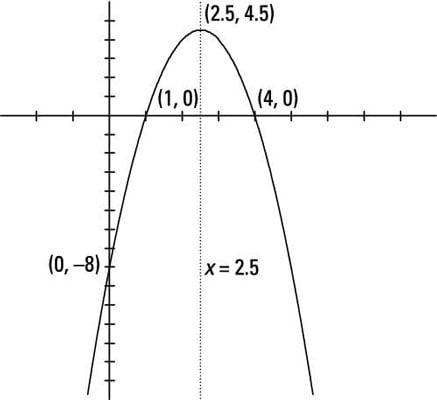
The intercepts are at (0, –8), (4, 0), and (1, 0). The parabola opens downward because –2 is negative. The vertex is at (2.5, 4.5), and the equation of the axis of symmetry is x = 2.5.

