A function has an infinite number of antiderivatives. In the example given here, you look at a particular antiderivative on the TI-Nspire and then see how to use a slider to investigate an entire family of curves defined by an antiderivative.
Use the TI-Nspire definite integral template
To graph the antiderivative of y = x3 – 3x2 – 2x + 6, follow these steps:
Press [CTRL][G] to open the entry line, then graph y = x3 – 3x2 – 2x + 6.

Press
to open the Math template, highlight the definite integral template, and press [ENTER].
See the first screen.
Press [0] to input the lower limit of the definite integral template, and then press [TAB] to move to the upper-limit field. Press [X] and then press [TAB] to move to the integral field.
Type f1(x) or press [VAR] and select f1 from the list of variables, then press [TAB] again to move to the next field of the definite integral template.
Type x in the last field and press [ENTER] to graph the antiderivative.
It may take a few seconds for the graph to form on a handheld.

The antiderivative that is graphed here is defined by the equation y = 1/4x4 – x3 – x2 – 6x.
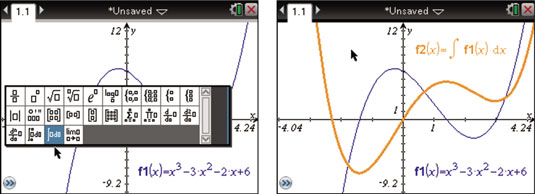
This equation is based on the general solution y = 1/4x4 – x3 – x2 – 6x + C with C = 0.
Use the indefinite integral template on TI-Nspire CAS

You can also use TI-Nspire CAS to graph this antiderivative using the indefinite integral template, also found in the Math template accessed by pressing
To add a dynamic element, try inserting a slider defined by the variable c. As shown in the first screen, use the definite integral template to graph the antiderivative as before. Then add + c in the equation for the purpose of investigating the family of curves given by the antiderivative of y = x3 – 3x2 – 2x + 6.
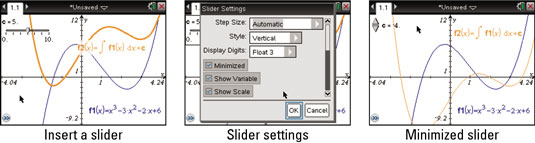
Right-click the slider and change the settings to Minimized (see the second screen). As you see in the last screen, you can click the slider and watch the graph of the derivative translate vertically.






