You can use Pythagorean identities to find the trig function of an angle if you know one trig function of the angle and are looking for another. For example, if you know the sine of an angle, you can use the first Pythagorean identity to find the cosine of the angle. In fact, you can find whatever you're asked to find if all you have is the value of one trig function and the understanding of what quadrant the angle θ is in.
The three Pythagorean identities are
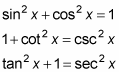
Here's an example:
If you know that
by following these steps:
Plug what you know into the appropriate Pythagorean identity.
Because you're using sine and cosine, you use the first identity:

Plug in the values you know to get

Isolate the trig function with the variable on one side.
First square the sine value to get 576/625, giving you

Subtract 576/625 from both sides (Hint: You need to find a common denominator):

Figure the square root both sides (taking both the positive and negative square roots) to solve.
You now have

But you can have only one solution because of the constraint

you're given in the problem.
Draw a picture of the unit circle so you can visualize the angle.
Because

the angle lies in quadrant II, so the cosine of θ must be negative. You have your answer:







