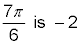You can determine the trig functions for any angles found on the unit circle — any that are graphed in standard position (meaning the vertex of the angle is at the origin, and the initial side lies along the positive x-axis). You use the rules for reference angles, the values of the functions of certain acute angles, and the rule for the signs of the functions.
Now, armed with all the necessary information, find the tangent of 300 degrees.
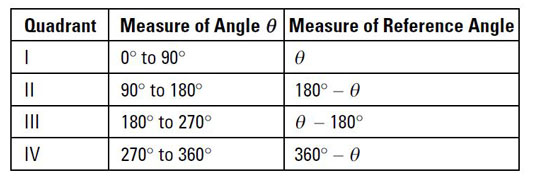
Find the reference angle.
Using the top chart, you can see that a 300-degree angle has its terminal side in the fourth quadrant, so you find the reference angle by subtracting 300 from 360. Therefore, the measure of the reference angle is 60 degrees.
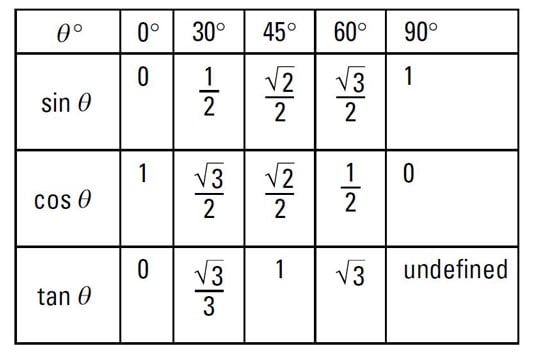
Find the numerical value of the tangent.
Using the middle chart, you see that the numerical value of the tangent of 60 degrees is
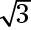
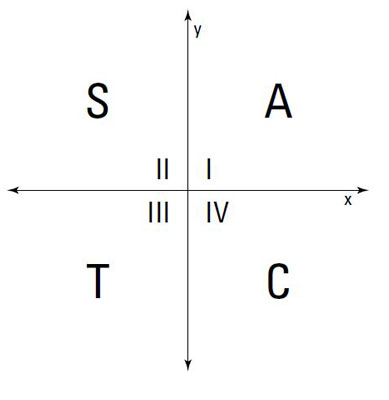
Find the sign of the tangent.
Because a 300-degree angle is in the fourth quadrant, and angles in that quadrant have negative tangents (refer to the preceding section), the tangent of 300 degrees is
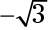
To try your hand at working with radians, find the cosecant of
Find the reference angle.
To use the top chart, you need to determine the degree equivalence for an angle measuring
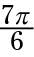
Using the formula for converting from radians to degrees, you get that
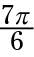
is equivalent to 210°. This angle is in the third quadrant, so, going back to radians, you find the reference angle by subtracting π from
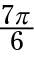
resulting in
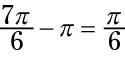
Find the numerical value of the cosecant.
In the middle chart 2, the cosecant doesn’t appear. However, the reciprocal of the cosecant is sine. So find the value of the sine, and use its reciprocal. The sine of
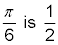
which means that the cosecant of
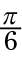
is 2 (the reciprocal).
Find the sign of the cosecant.
In the third quadrant, the cosecant of an angle is negative, so the cosecant of