As with sine and cosine, you can rely on formulas to find the tangent of a sum or a difference of angles. The main difference is that you can't read tangents directly from the coordinates of points on the unit circle, as you can with sine and cosine, because each point represents
All hope isn't lost, however, because the tangent of an angle θ is defined as sin θ /cos θ. Because the sine of the angle is the y-coordinate and the cosine is the x-coordinate, you can express the tangent in terms of x and y on the unit circle as y/x.
Here are the formulas you need to find the tangent of a sum or difference of angles:
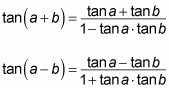
You should memorize these sweet little formulas, because then you won't have to use the sum and difference formulas for sine and cosine in the middle of a tangent problem, saving you time in the long run. If you choose not to memorize these two formulas, you can derive them by remembering these equations:
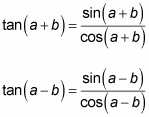
The sum and difference formulas for tangent work in similar ways to those of the sine and cosine formulas. You can use the formulas to solve a variety of problems, such as how to find the tangent of an angle that isn't marked on the unit circle. You can do so as long as the angle can be written as the sum or difference of special angles.
For example, to find the exact value of tan 105 degrees, follow these steps (note that the angle 105 degrees is in quadrant II):
Rewrite the given angle, using the information from special right-triangle angles.
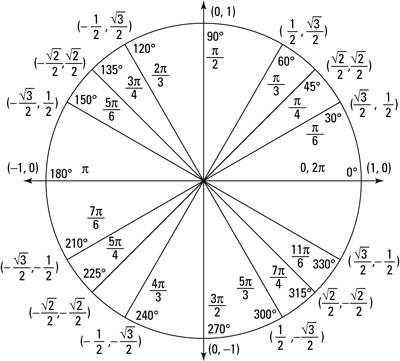 The whole unit circle
The whole unit circleRefer to the unit circle, noting that it's built from the special right triangles, to find a combination of angles that add or subtract to get 105 degrees. You can choose from 240 degrees – 135 degrees, 330 degrees – 225 degrees, and so on. This example uses 60 degrees + 45 degrees.

Because the angle is rewritten with addition, you need to use the sum formula for tangent.
Plug the information you know into the appropriate formula.

Use the unit circle to look up the sine and cosine values that you need.
To find tan 60º, you must locate 60° on the unit circle and then use the corresponding point on the unit circle to obtain the sine and cosine values to calculate the tangent:

Substitute the trig values from Step 3 into the formula.
This step gives you

which simplifies to

Rationalize the denominator.
You can't leave the square root in the denominator of a fraction. Because the denominator is a binomial (the sum or difference of two terms), you must multiply both the numerator and denominator by the conjugate of the denominator. The conjugate of a + b is a – b, and vice versa.


Simplify the rationalized fraction to find the exact value of tangent.
Combine like terms to get

Make sure you fully simplify this fraction to get







