Because the binomial distribution is so commonly used, statisticians went ahead and did all the grunt work to figure out nice, easy formulas for finding its mean, variance, and standard deviation. The following results are what came out of it.
If X has a binomial distribution with n trials and probability of success p on each trial, then:
The mean of X is
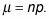
The variance of X is
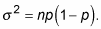
The standard deviation of X is

For example, suppose you flip a fair coin 100 times and let X be the number of heads; then X has a binomial distribution with n = 100 and p = 0.50. Its mean is
heads (which makes sense, because if you flip a coin 100 times, you would expect to get 50 heads). The variance of X is
which is in square units (so you can't interpret it); and the standard deviation is the square root of the variance, which is 5. That means when you flip a coin 100 times, and do that over and over, the average number of heads you'll get is 50, and you can expect that to vary by about 5 heads on average.
The formula for the mean of a binomial distribution has intuitive meaning. The p in the formula represents the probability of a success, yes, but it also represents the proportion of successes you can expect in n trials. Therefore, the total number of successes you can expect — that is, the mean of X — is
The formula for variance has somewhat of an intuitive meaning as well. The only variability in the outcomes of each trial is between success (with probability p) and failure (with probability 1 – p). Over n trials, the variance of the number of successes/failures is measured by
The standard deviation is just the square root.






