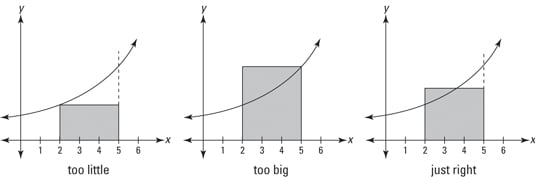
The graph on the left shows a rectangle whose area is clearly less than the area under the curve between 2 and 5. This rectangle has a height equal to the lowest point on the curve in the interval from 2 to 5.
The middle graph shows a rectangle whose height equals the highest point on the curve. Its area is clearly greater than the area under the curve. By now you’re thinking, “Isn’t there a rectangle taller than the short one and shorter than the tall one whose area is the same as the area under the curve?” Of course. And this rectangle obviously crosses the curve somewhere in the interval. This so-called mean value rectangle, shown on the right, basically sums up the Mean Value Theorem for Integrals.
It’s really just common sense. But here’s the mumbo jumbo.
The mean value theorem for integrals: If f (x) is a continuous function on the closed interval [a, b], then there exists a number c in the closed interval such that
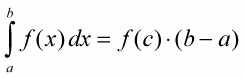
The theorem basically just guarantees the existence of the mean value rectangle.
The area of the mean value rectangle — which is the same as the area under the curve — equals length times width, or base times height, right?
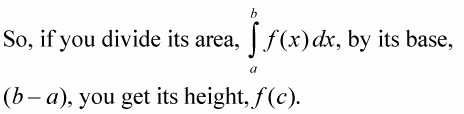
This height is the average value of the function over the interval in question.

Here’s an example. What’s the average speed of a car between t = 9 seconds and t = 16 seconds whose speed in feet per second is given by the function,
According to the definition of average value, this average speed is given by
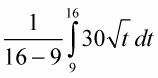
-
Determine the area under the curve between 9 and 16.
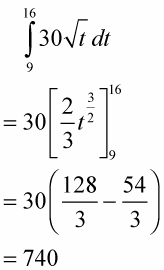
This area, by the way, is the total distance traveled from 9 to 16 seconds. Do you see why? Consider the mean value rectangle for this problem. Its height is a speed (because the function values, or heights, are speeds) and its base is an amount of time, so its area is speed times time which equals distance. Alternatively, recall that the derivative of position is velocity. So, the antiderivative of velocity — what you just did in this step — is position, and the change of position from 9 to 16 seconds gives the total distance traveled.
-
Divide this area, total distance, by the time interval from 9 to 16, namely 7.
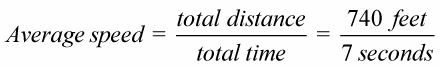
≈ 105.7 feet per second
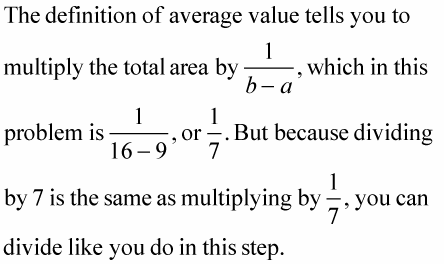
It makes more sense to think about these problems in terms of division: area equals base times height, so the height of the mean value rectangle equals its area divided by its base.

