When you know the lengths of two of a triangle’s sides plus the measure of the angle between those sides (SAS), you can find the area of the triangle. This method requires a little trigonometry — you have to find the sine of the angle involved. But the formula is really straightforward.
If triangle ABC has sides measuring a, b, and c opposite the respective angles, then you can find the area with one of these formulas:
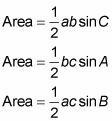
For example, look at the 30-60-90 right triangle in the following figure.
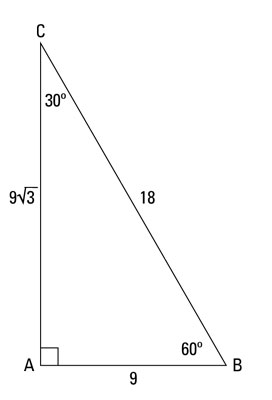
First, find the area by using angle B and the two sides forming it.
Choose the correct version of the formula.

Find the sine of the angle.

Substitute the values into the formula and simplify.

Now find the area by using angle C and the two sides forming it.
Choose the correct version of the formula.

Find the sine of the angle.

Substitute the values into the formula and simplify.

Using the method involving angle A gives you the same result, of course. For a quick comparison, just use the formula
to find the area, because you’re dealing with a right triangle:
The methods all produce the same result.






