You can use Heron’s Formula to find the area of the triangle, even if you only know the sides of the triangle and not any of the angles (which is called SSS, or side-side-side, in trigonometry terms). Heron's formula is handy, for instance, if you need to find the maximum area possible given the sum of sides of a triangle.
For example, suppose that you have 240 yards of fencing, and you decide to build a triangular corral for your llama. Why triangular? You heard that llamas favor the shape, of course. You want the llama to have enough room to run around, so you need to know the area. What should the lengths of the triangle’s sides be? You can solve this little problem by using Heron’s Formula for the area of a triangle.
Heron’s formula says that if a triangle ABC has sides of lengths a, b, and c opposite the respective angles, and you let the semiperimeter, s, represent half of the triangle’s perimeter, then the area of the triangle is
In the problem of the fencing and the llama, you have many ways to make a triangular corral from 240 yards of fencing. The following figure shows a few of the possibilities. Notice that in each case, the lengths of the sides add up to 240. For the sake of this problem, don’t worry about a gate.
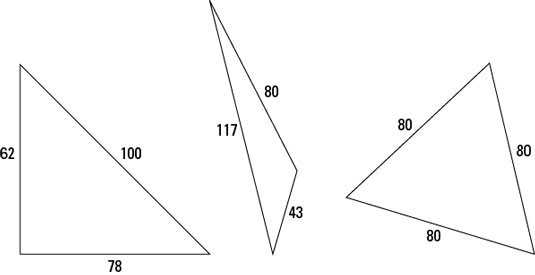
Which triangle has the greatest area? Obviously, one of them is a bit on the scrawny side, even though it uses up 240 yards of fencing, like the others. Here’s how to compute the areas for the three triangles.
Find the semiperimeter, s, for each triangle.
Referring to the preceding figure:

Not surprisingly, all the semiperimeters are the same, because all the perimeters are 240.
Use Heron’s Formula to find each area.
Again, referring to the preceding figure:

The triangle on the right has the greatest area. Of the shapes in the figure, that triangle is the best. But you may be wondering whether another shape gives more area than that one. The answer: no. With calculus, you can prove that an equilateral triangle gives you the greatest possible area with any amount of fencing. Without calculus, you just have to try a bunch of shapes to convince yourself.






