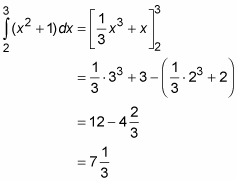The Fundamental Theorem of Calculus has a shortcut version that makes finding the area under a curve a snap. Here it is. Let F be any antiderivative of the function f; then
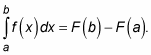
With this version of the Fundamental Theorem, you can easily compute a definite integral like

You could get this area with two different methods that involve area functions. First, you could determine the area function for this parabola that begins sweeping out area at x = 2, and then compute that area function’s output when x = 3. Second, you could determine the area function for the parabola that begins sweeping out area at x = 0, and then use that area function to subtract the area from 0 to 2 from the area from 0 to 3.
The beauty of the shortcut theorem is that you don’t have to use an area function like
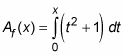
or any other area function.
You just find any antiderivative, F(x), of your function, and do the subtraction, F(b) – F(a). The simplest antiderivative to use is the one where C = 0. So, here’s how you use the theorem to find the area under the parabola from 2 to 3.

and thus,