Every function that’s continuous on a closed interval has an absolute maximum value and an absolute minimum value (the absolute extrema) in that interval — in other words, a highest and lowest point — though there can be a tie for the highest or lowest value.
A closed interval like [2, 5] includes the endpoints 2 and 5. An open interval like (2, 5) excludes the endpoints.
Finding the absolute max and min is a snap. All you do is compute the critical numbers of the function in the given interval, determine the height of the function at each critical number, and then figure the height of the function at the two endpoints of the interval. The greatest of this set of heights is the absolute max; and the least, of course, is the absolute min. Here’s an example:
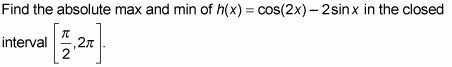
Start by finding the critical numbers of h in the open interval,

Compute the function values (the heights) at each critical number.
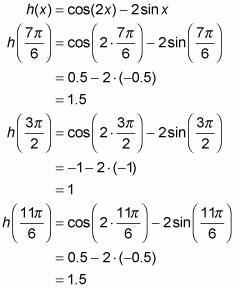
Determine the function values at the endpoints of the interval.
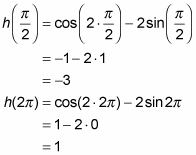
So, from Steps 2 and 3, you’ve found five heights: 1.5, 1, 1.5, –3, and 1. The largest number in this list, 1.5, is the absolute max; the smallest, –3, is the absolute min.

an endpoint extremum.
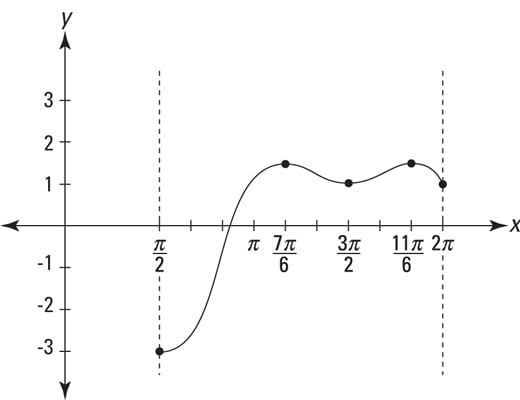
A couple observations:
However, if you only want to find the absolute extrema on a closed interval, you don’t have to pay any attention to whether critical points are local maxes, mins, or neither. And thus you don’t have to bother to use the first or second derivative tests. All you have to do is determine the heights at the critical numbers and at the endpoints and then pick the largest and smallest numbers from this list.
Second, the absolute max and min in the given interval tell you nothing about how the function behaves outside the interval.


