It's a good idea to familiarize yourself with a set of formulas that change sums to products. Sum-to-product formulas are useful to help you find the sum of two trig values that aren't on the unit circle. Of course, these formulas work only if the sum or difference of the two angles ends up being an angle from the special triangles:
Here are the sum/difference-to-product identities:
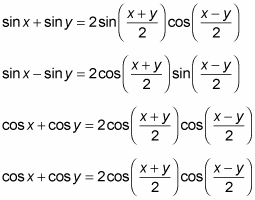
For example, say you're asked to find
without a calculator. You're stuck, right? Well, not exactly. Because you're asked to find the sum of two trig functions whose angles aren't special angles, you can change this to a product by using the sum to product formulas. Follow these steps:
Change the sum to a product.
Because you're asked to find the sum of two sine functions, use this equation:

This step gives you

Simplify the result.
Combining like terms and dividing gives you

Those angles are represented on the unit circle, so continue to the next step.
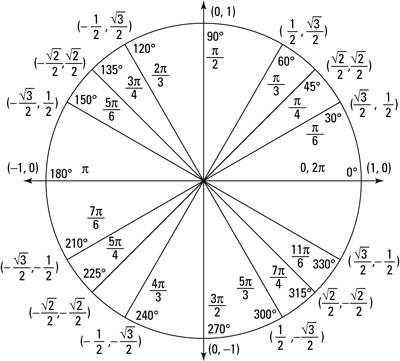 The whole unit circle
The whole unit circleUse the unit circle to simplify further.

Substituting those values in, you get







