How to Evaluate an Improper Integral that Is Vertically Infinite

Improper integrals are useful for solving a variety of problems. A vertically infinite improper integral contains at least one vertical asymptote. Vertically infinite improper integrals are harder to recognize than those that are horizontally infinite. An integral of this type contains at least one vertical asymptote in the area that you’re measuring. (A vertical asymptote is a value of x where f(x) equals either or –.) The asymptote may be a limit of integration or it may fall someplace between the two limits of integration.

Don’t try to slide by and evaluate improper integrals as proper integrals. In most cases, you’ll get the wrong answer!

There are two cases where you’ll need to handle vertically infinite improper integrals.

Handling asymptotic limits of integration

Suppose that you want to evaluate the following integral:

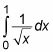
At first glance, you may be tempted to evaluate this as a proper integral. But this function has an asymptote at x = 0. The presence of an asymptote at one of the limits of integration forces you to evaluate this one as an improper integral.

1. Express the integral as the limit of a proper integral:

   

   Notice that in this limit, c approaches 0 from the right — that is, from the positive side — because this is the direction of approach from inside the limits of integration. (That’s what the little plus sign in the limit means.)

2. Evaluate the integral:

   This integral is easily evaluated as

   

   using the Power Rule:

   

3. Evaluate the limit:

   

   At this point, direct substitution provides you with your final answer:

   = 2

Piecing together discontinuous integrands

If a function is continuous on an interval, it’s also integrable on that interval. Some integrals that are vertically infinite have asymptotes not at the edges but someplace in the middle. The result is a discontinuous integrand — that is, a function with a discontinuity on the interval that you’re trying to integrate.

Discontinuous integrands are the trickiest improper integrals to spot — you really need to know how the graph of the function that you’re integrating behaves.

To evaluate an improper integral of this type, separate it at each asymptote into two or more integrals. Then evaluate each of the resulting integrals as an improper integral.

For example, suppose that you want to evaluate the following integral:

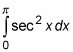
Because the graph of sec x contains an asymptote at

the graph of sec² x has an asymptote in the same place. For example, a graph of the improper integral

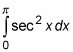
in shown in this figure.

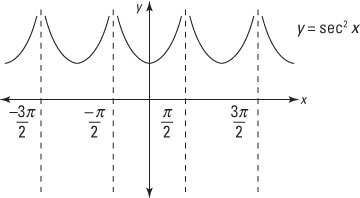
To evaluate this integral, break it into two integrals at the value of x where the asymptote is located:

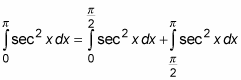
Now evaluate the sum of the two resulting improper integrals.

You can save yourself a lot of work by noticing when two regions are symmetrical. In this case, the asymptote at

splits the shaded area into two symmetrical regions. So you can find one integral and then double it to get your answer:

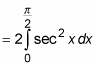
Now evaluate this integral:

1. Express the integral as the limit of a proper integral:

   

   In this case, the vertical asymptote is at the upper limit of integration, so c approaches

   

   from the left — that is, from inside the interval where you’re measuring the area.

2. Evaluate the integral:

   

3. Evaluate the limit:

   Note that

   

   is undefined, because the function tan x has an asymptote at

   

   so the limit does not exist (DNE). Therefore, the integral that you’re trying to evaluate also does not exist because the area that it represents is infinite.