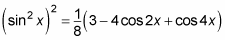Power-reducing formulas allow you to get rid of exponents on trig functions so you can solve for an angle's measure. This ability comes in very handy in calculus.
At some point, you'll be asked to rewrite an expression using only the first power of a given trig function — either sine, cosine, or tangent — with the help of power-reducing formulas, because exponents can really complicate trig functions in calculus when you're attempting to integrate functions.
In some cases, when the function is raised to the fourth power or higher, you may have to apply the power-reducing formulas more than once to eliminate all the exponents. You can use the following three power-reducing formulas to accomplish the elimination task:
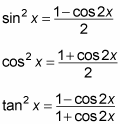
For example, follow these steps to express sin4 x without exponents:
Apply the power-reducing formula to the trig function.
First, realize that sin4 x = (sin2 x)2. Because the problem requires the reduction of sin4 x, you must apply the power-reducing formula twice. The first application gives you the following:
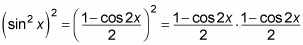
FOIL the numerator.
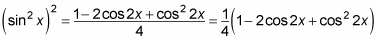
Apply the power-reducing formula again (if necessary).
Because the equation contains cos2 2x, you must apply the power-reducing formula for cosine.
Because writing a power-reducing formula inside a power-reducing formula is very confusing, find out what cos2 2x is by itself first and then plug it back in:
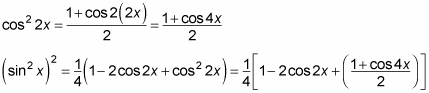
Simplify to get your result.
Factor out 1/2 from everything inside the brackets so that you don't have fractions both outside and inside the brackets. This step gives you
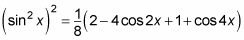
Combine like terms to get