If you can find the midpoint of a segment, you can divide it into two equal parts. Finding the middle of each of the two equal parts allows you to find the points needed to divide the entire segment into four equal parts. Finding the middle of each of these segments gives you eight equal parts, and so on.
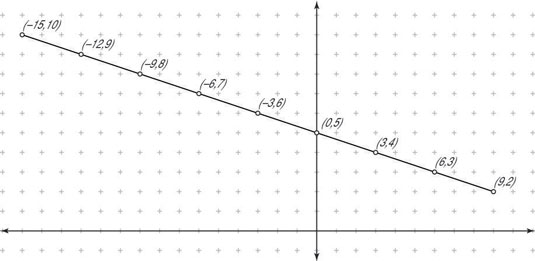
For example, to divide the segment with endpoints (–15,10) and (9,2) into eight equal parts, find the various midpoints like so:
The midpoint of the main segment from (–15,10) to (9,2) is (–3,6).
The midpoint of half of the main segment, from (–15,10) to (–3,6), is (–9,8), and the midpoint of the other half of the main segment, from (–3,6) to (9,2), is (3,4).
The midpoints of the four segments determined above are (–12,9), (–6,7), (0,5), and (6,3).
The figure shows the coordinates of the points that divide this line segment into eight equal parts.
Using the midpoint method is fine, as long as you just want to divide a segment into an even number of equal segments. But your job isn't always so easy. For instance, you may need to divide a segment into three equal parts, five equal parts, or some other odd number of equal parts.
To find a point that isn't equidistant from the endpoints of a segment, just use this formula:
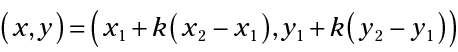
In this formula, (x1,y1) is the endpoint where you're starting, (x2,y2) is the other endpoint, and k is the fractional part of the segment you want.
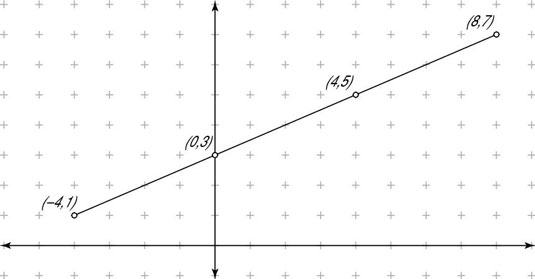
So, to find the coordinates that divide the segment with endpoints (–4,1) and (8,7) into three equal parts, first find the point that's one-third of the distance from (–4,1) to the other endpoint, and then find the point that's two-thirds of the distance from (–4,1) to the other endpoint. The following steps show you how.
To find the point that's one-third of the distance from (–4,1) to the other endpoint, (8,7):
Replace x1 with –4, x2 with 8, y1 with 1, y2 with 7, and k with 1/3.

Subtract the values in the inner parentheses.

Do the multiplication and then add the results to get the coordinates.
=(–4 + 4,1 + 2) = (0,3)
To find the point that's two-thirds of the distance from (–4,1) to the other endpoint, (8,7):
Replace x1 with –4, x2 with 8, y1 with 1, y2 with 7, and k with 2/3.

Subtract the values in the inner parentheses.

Do the multiplication and then add the results to get the coordinates.
=(–4 + 8,1 + 4) = (4,5)
The following figure shows the graph of this line segment and the points that divide it into three equal parts.