The theory of price elasticity is one of the major tenets of managerial economics. That theory maintains that long-term success and profitability depend upon ideal pricing, or producing a good to the point where the additional revenue of an extra unit of output equals the additional cost of producing that unit; in other words, producing where marginal revenue equals marginal cost.
You can derive marginal revenue from the firm’s demand. However, an easier method of deriving marginal revenue is to use the price elasticity of demand. The relationship between marginal revenue and the price elasticity of demand is:
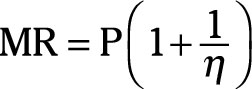
where MR is marginal revenue, P is the good’s price, and ç is the price elasticity of demand.
Maximizing profit requires marginal revenue equals marginal cost, so
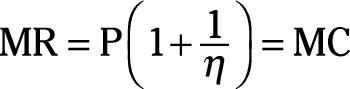
Rearranging the previous equation yields
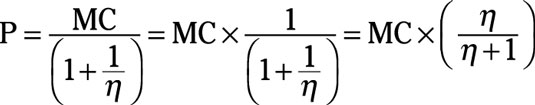
Thus, the profit-maximizing price equals
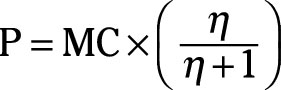
Remember that the price elasticity of demand is a negative number because an inverse relationship exists between price and quantity demanded.
Your company produces a good at a constant marginal cost of $6.00. The price elasticity of demand for the good is –4.0. In order to determine the profit-maximizing price, you follow these steps:
Substitute $6.00 for MC and –4.0 for ç.

Calculate the value in the parentheses.

Multiply values to yield a price of $8.00.






