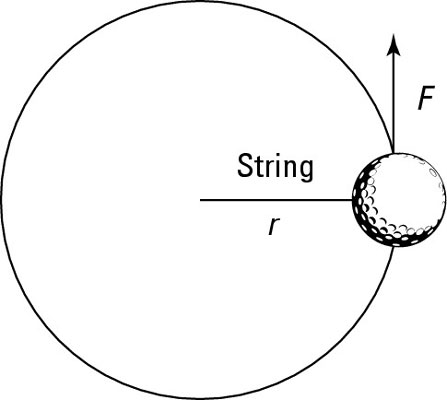
Using physics, you can convert linear force to angular torque. For example, say that you’re whirling a ball in a circle on the end of a string, as shown in the figure. You apply a tangential force (along the circle) to the ball, making it speed up (keep in mind that this force is not directed toward the center of the circle, as when you have a centripetal force). You want to write Newton’s second law in terms of torque rather than force.
Start by working with only the magnitudes of the vector quantities, saying that
F = ma
To put this equation in terms of angular quantities, such as torque, multiply by the radius of the circle, r:
Fr = mra
Because you’re applying tangential force to the ball, the force and the circle’s radius are at right angles (see the figure), so you can replace Fr with torque:
(where torque is represented by the Greek letter tau). You’re now partly done making the transition to rotational motion. Instead of working with linear force, you’re working with torque, which is linear force’s rotational analog.






