Basic Math & Pre-Algebra All-in-One For Dummies (+ Chapter Quizzes Online)
Explore Book Buy On AmazonThis distinction between volume and capacity is subtle — you can measure both in cm3, although confusingly you can also measure capacity in milliliters, each of which is the same size as 1 cm3. A liter contains 1,000 millilitres, and a cubic meter contains 1,000 liters.
Incidentally, a cubic centimeter is the volume of a cube which has edges that are one centimeter long — about the size of a normal die.
For the numeracy curriculum, you may need to work out the volume of a cuboid or shoebox. You normally know the width, height and depth of the box. To work out the volume, you simply times the three numbers together.A classic problem in numeracy exams involves working out how many small boxes fit into a bigger box. This kind of packing problem has real-life applications (how many DVDs can you fit into a box? Will this crate hold all the copies of Basic Maths For Dummies you want to send to your friends around the world?) and is quite straightforward.
In an exam, you normally know the orientation — or which way round you need to pack the little boxes into the big box. Follow these steps to work out how to fit little boxes into a bigger box:
-
Work out how many boxes you can fit along the front of the box.
Divide the width of the big box by the width of one small box and write down the result. If you get a whole number answer, great! If not, round down, because even if your answer is 5.99, you can’t squeeze a sixth little box into the crate.
-
Work out how many boxes you can fit along the side of the box.
Divide the depth of the big box by the depth of the little box and write down the answer. Round down if you don’t have a whole number.
-
Work out how many boxes you can fit going up the box.
Divide the height of the big box by the height of the small box and write down the number. Round down if you need to.
-
Times the three numbers together.
That’s your answer!
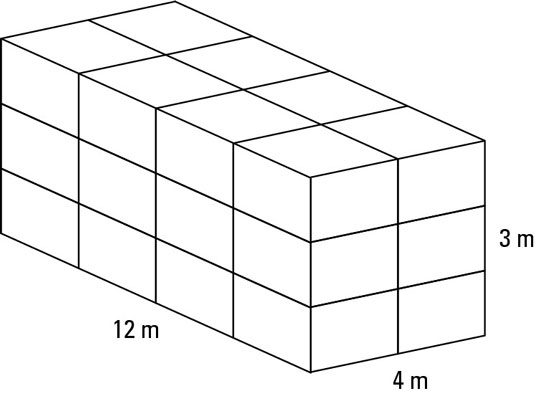
A crate is 4 meters wide, 12 meters long and 3 meters deep. You want to fill it with boxes that are 2 meters wide, 3 meters long and 1 meter deep. How many boxes will fit in the crate?
-
You can fit two boxes along the width of the crate.
-
You can fit four boxes along the length of the crate.
-
You can fit three boxes along the depth of the crate.
-
You need to times those numbers together.
2 x 4 x 3 = 8 x 3 = 24.
-
You can fit 24 boxes into the crate.