In physics, if a force on an object has a component in the same direction as the motion, the work that force does on the object is positive. If a force on an object has a component in the opposite direction to the motion, the work done by that force on the object is negative.
Consider this example: You’ve just gone out and bought the biggest television your house can handle. You finally get the TV home, and you have to lift it up the porch stairs. It’s a heavy one — about 100 kilograms, or 220 pounds — and as you lift it up the first few stairs, a distance of about 0.50 meters, you think you should’ve gotten some help because of how much work you’re doing. (Note: The force you apply in lifting the TV is equal to its weight, or 100 kilograms times g, the acceleration due to gravity; theta is 0 degrees because your lifting force and the displacement are in the same direction, the direction in which the TV is moving.)

However, as you get the TV to the top of the steps, your back decides that you’re carrying too much weight and advises you to drop it. Slowly, you lower the TV back to its original position (with no acceleration so that the force you apply is equal and opposite to the downward gravitational force on the TV) and take a breather. How much work did you do on the way down? Believe it or not, you did negative work on the TV, because the force you applied (still upward) was in the opposite direction of travel (downward). In this case,
Here’s what you get when you solve for the work:
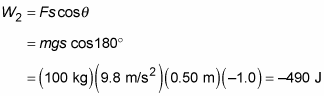
The net work you’ve done is W = W1 + W2 = 0 joules, or zero work. That makes sense, because the TV is right back where it started.
Because the force of friction always acts to oppose the motion, the work done by frictional forces is always negative.

