If you apply force at an angle instead of parallel to the direction of motion, you have to supply more force to perform the same amount of work. You can use physics to calculate how much work is required, for example, when you drag an object using a tow rope, as the figure shows.
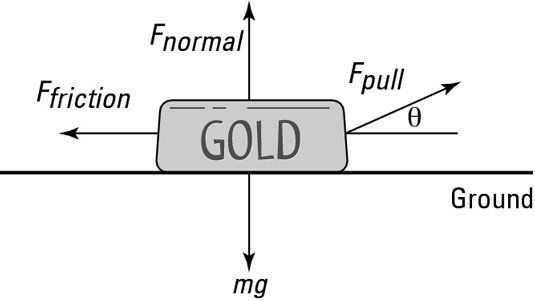
When you’re pulling at an angle theta, you’re not applying a force in the exact same direction as the direction of motion. To find the work in this case, all you have to do is find the component of the force along the direction of motion or displacement. Work properly defined is the force along the direction of displacement multiplied by the magnitude of the displacement, s:
Say that you use a rope to drag a gold ingot, and the rope is at an angle of 10 degrees from the ground instead of parallel. In this example, theta = 10 degrees. If you want to apply the same amount of force parallel to the ground as before, then you would need the component of your force that is in the direction of the displacement to be the same as if you were applying a parallel force — in this case, 2,450 newtons. This means that
If you solve for the magnitude of your force, you have
If you pull at a 10-degree angle, you have to supply about 40 extra newtons of force. But will you end up doing the same amount of work? You would if you pulled with this force. But think about the situation a bit more — you actually don’t have to do as much work.
If you pull at an angle, the component of the force you apply that’s directed along the floor — in the direction of the displacement — does the work. The component of the force you apply that’s directed at right angles to this — straight up — does no work, but it does go some way toward lifting the ingot (or whatever you’re towing). The force isn’t big enough to lift the ingot clean off the ground, but it does reduce its normal force with the ground, and you know what that means: less friction.
Work out how much frictional force you have if you drag your ingot with a rope that’s at a 10-degree angle. The coefficient of friction is the same as if you are pushing the ingot, but now the normal force with the ground is given by the weight of the ingot minus the upward component of the force you supply. Therefore, the force of friction is given by
Here, the vertical component of the force you apply to the ingot is given by
The force of friction must be smaller than if you were pulling the ingot parallel to the ground because the normal force is smaller — you can already see that you need to do less work to move the ingot.
Because you want to do the least amount of work, you want to drag the ingot across the ground with the smallest force needed to overcome friction. So set the horizontal component of your force equal to the force of friction:
Now plug in the frictional force, which gives you the following:
If you rearrange this equation to solve for Fpull, you can find the magnitude of the force you need to apply:

This is slightly smaller than the force you’d have to apply if you pulled the ingot straight on. Now, say that you want to move the ingot to your house, which is 3 kilometers away. If the rope is at a 10-degree angle, the work you’d do in pulling the ingot over a horizontal distance of 3 kilometers (3,000 meters) would be
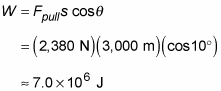
If you pulled the ingot straight on, you would use 7.35 x 106 J. So you see, you have to do less work if you pull at an angle because there’s less frictional force to overcome.






