When determining the trig function values of angles graphed in standard position on a circle whose center is at the origin, you don’t have to have a unit circle to calculate coordinates. You can use a circle with any radius, as long as the center is at the origin.
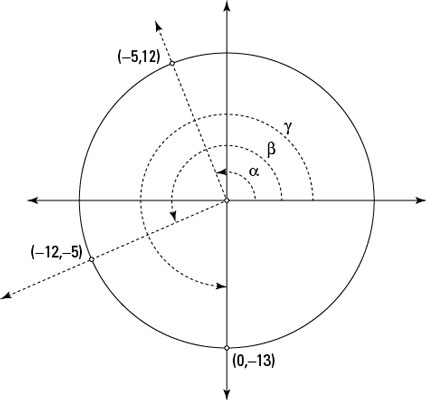
Using the angles in the preceding figure, you can follow these steps to find the sine of angle α:
1. Find the x- and y-coordinates of the point where the terminal side of the angle intersects with the circle.
The coordinates are x = –5 and y = 12.
2. Determine the radius of the circle.
The equation of a circle with its center at the origin is x2 + y2 = r2. Replacing the x and y in this equation with –5 and 12, respectively, you get (–5)2 + (12)2 = 25 + 144 = 169 = r2. The square root of 169 is 13, so the radius is 13.
3. Determine the ratio for the function and substitute in the values.

Next, using the angles in the figure, find the cotangent of angle β.
Find the x- and y-coordinates of the point where the terminal side of the angle intersects with the circle.
The coordinates are x = –12 and y = –5.
The cotangent function uses only the x- and y-coordinates, so you don’t need to solve for the radius.
Determine the ratio for the function and substitute in the values.
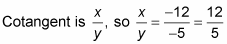
Now, using the angles in the preceding figure, find the secant of angle γ.
1. Find the x- and y-coordinates of the point where the terminal side of the angle intersects with the circle.
The coordinates are x = 0 and y = –13.
Determine the radius of the circle.
From the first example, the radius is 13.
Determine the ratio for the function and substitute in the values.
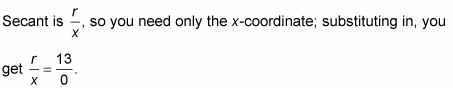
This ratio is undefined, which means that angle γ has no secant.

