Measuring angles in degrees for the sum and difference formulas for sine is easier than measuring in radians, because adding and subtracting degrees is much easier than adding and subtracting radians. Adding and subtracting angles in radians requires finding a common denominator. Moreover, evaluating trig functions requires you to work backward from a common denominator to split the angle into two fractions with different denominators.
If you look really closely, you'll notice that 45 degrees – 30 degrees = 15 degrees, and 45 degrees + 30 degrees = 75 degrees. For the angles you can rewrite as the sum or difference of special angles, here are the sum and difference formulas for sine:
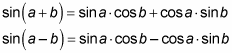
As an example, follow these steps to find the sine of 135 degrees:
Rewrite the angle, using the special angles from right triangles.
One way to rewrite 135 degrees is 90 degrees + 45 degrees.
Choose the appropriate sum or difference formula.
The example from Step 1 uses addition, so you want to use the sum formula, not the difference formula:

Plug the information you know into the formula.
You know that

Therefore, a = 90 degrees and b = 45 degrees.
The formula gives you

Use the unit circle to look up the sine and cosine values you need.
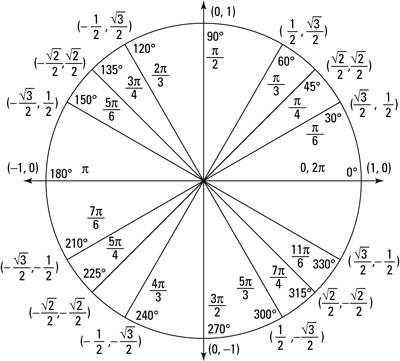 The whole unit circle
The whole unit circleYou now have

Multiply and simplify to find the final answer.
You end up with







