How to Calculate the Momentum of Inertia for Different Shapes and Solids

In physics, when you calculate an object’s moment of inertia, you need to consider not only the mass of the object but also how the mass is distributed. For example, if two disks have the same mass but one has all the mass around the rim and the other is solid, then the disks would have different moments of inertia.

Calculating moments of inertia is fairly simple if you only have to examine the orbital motion of small point-like objects, where all the mass is concentrated at one particular point at a given radius r. For instance, for a golf ball you’re whirling around on a string, the moment of inertia depends on the radius of the circle the ball is spinning in:

I = mr²

Here, r is the radius of the circle, from the center of rotation to the point at which all the mass of the golf ball is concentrated.

Crunching the numbers can get a little sticky when you enter the non–golf ball world, however, because you may not be sure of which radius to use. What if you’re spinning a rod around? All the mass of the rod isn’t concentrated at a single radius. When you have an extended object, such as a rod, each bit of mass is at a different radius. You don’t have an easy way to deal with this, so you have to sum up the contribution of each particle of mass at each different radius like this:

You can use this concept of adding up the moments of inertia of all the elements to get the total in order to work out the moment of inertia of any distribution of mass. Here’s an example using two point masses, which is a bit more complex than a single point mass. Say you have two golf balls, and you want to know what their combined moment of inertia is. If you have a golf ball at radius r₁ and another at r₂, the total moment of inertia is

So how do you find the moment of inertia of, say, a disk rotating around an axis stuck through its center? You have to break the disk up into tiny balls and add them all up. You complete this using the calculus process of integration.

The shapes corresponding to the moments of inertia in the table.

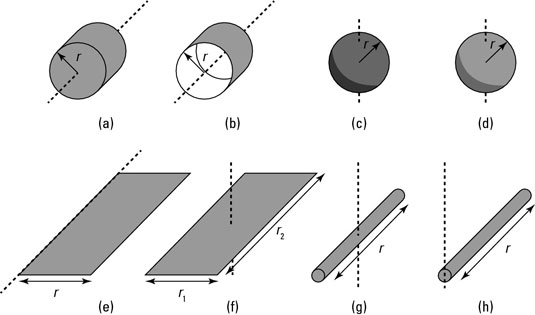
Trusty physicists have already completed this task for many standard shapes; The following table provides a list of objects you’re likely to encounter, and their moments of inertia. The figure depicts the shapes that these moments of inertia correspond to.