According to the laws of physics, when a projectile flies into the air, its trajectory is shaped by Earth’s gravitational pull. Because the force of gravity only acts downward — that is, in the vertical direction — you can treat the vertical and horizontal components separately. As a result, you can calculate how far the projectile can travel straight up in the air.
Say, for example, that on your birthday, your friends give you just what you’ve always wanted: a cannon. It has a muzzle velocity of 860 meters/second, and it shoots 10-kilogram cannonballs. Anxious to show you how it works, your friends shoot it off with the cannon pointing straight up.
Everyone starts to guess how high it will go. Because you know your physics, you can figure this out almost exactly (ignoring air resistance).
You know the initial vertical velocity, vi, of the cannonball, and you know that gravity will accelerate it downward. How can you determine how high the ball will go? At the cannonball’s maximum height, its vertical velocity will be zero, and then it will head down to Earth again. Therefore, you can use the following equation for the cannonball’s highest point, where its vertical velocity will be zero:
You want to know the cannonball’s displacement from its initial position, so solve for s. This gives you
Plugging in what you know — vf is 0 meters/second, vi is 860 meters/second, and the acceleration is g downward (g being 9.8 meters/second2, the acceleration due to gravity on the surface of the Earth), or –g. You get this:
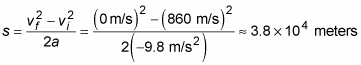
Whoa! The ball will go up 38 kilometers, or nearly 24 miles. Not bad for a birthday present. Theoretically, that 10kg (about 22 lb.) cannonball will come back down and land with a speed of 860 m/s, which means that a) everyone ought to stand back, and (b) if the shot was truly vertical, the returning cannonball might smash your cannon. Enjoy it while you can.






