In physics, displacement, which is a change in position, has a magnitude and a direction associated with it. When you have a change of position in a particular direction and of a particular distance, these are given by the magnitude and direction of the displacement vector.
Instead of writing displacement as s, you should write it as s, a vector (if you’re writing on paper, you can put an arrow over the s to signify its vector status). When you’re talking about displacement in the real world, direction is as important as distance.
For example, say your dreams have come true: You’re a big-time baseball or softball hero, slugging another line drive into the outfield. You take off for first base, which is 90 feet away. But 90 feet in which direction? Because you know how vital physics is, you happen to know that first base is 90 feet away at a 45-degree angle, as you can see in this figure.
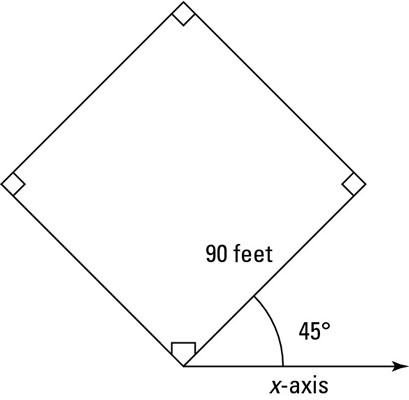
Now you’re set, all because you know that displacement is a vector. In this case, here’s the displacement vector:
s = 90 feet at 45 degrees
What’s that in components?
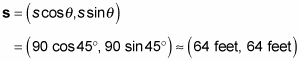
Sometimes, working with angles and magnitudes isn’t as easy as working with x and y components. For example, say that you’re at the park and ask directions to the nearest bench. The person you ask is very precise and deliberate and answers, “Go north 10.0 meters.”
“North 10.0 meters,” you say. “Thanks.”
“Then east 20.0 meters. Then north another 50.0 meters.”
“Hmm,” you say. “North 10.0 meters, then 20.0 meters east, and then another 50.0 meters east . . . I mean north. Is that right?”
“Then 60.0 meters east.”
You look at the person warily. “Is that it?”
“That’s it,” she says. “Nearest bench.”
Okay, time for some physics. The first step is to translate all that north and east business into x and y coordinates like this: (x, y). So assuming that the positive x-axis points east and the positive y-axis points north (as on a map), the first step is 10.0 meters north, which becomes the following (where all measurements are in meters):
(0, 10.0)
That is, the first step is 10.0 meters north, which translates into 10.0 meters in the positive y direction. Adding the second step, 20.0 meters east (the positive x direction), gives you

The third step is 50.0 meters north, and adding that gives you
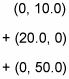
And finally, the fourth step is 60.0 meters east, which gives you

Whew. Okay, what’s the sum of all these vectors? You just add up the components:

So the resulting vector is (80.0, 60.0). Hmm, that seems a lot easier than the directions you got. Now you know what to do: proceed 80.0 meters east and 60.0 meters north. See how easy adding vectors together is?
You can, if you like, go even further. You have the displacement to the nearest bench in terms of x and y components. But it looks like you’ll have to walk 80.0 meters east and then 60.0 meters north to find the bench. Wouldn’t it be easier if you just knew the direction to the bench and the total distance? Then you could cut the corner and just walk in a straight line directly to the bench.
This is an example where it’s good to know how to convert from the (x, y) coordinate form of a vector into the magnitude-angle form. And you can do it with all the physics knowledge you have. Converting (80.0, 60.0) to the magnitude-angle form allows you to cut the corner when you walk to the bench, saving a few steps.
You know that the x and y components of a vector form a right triangle and that the total magnitude of the vector is equal to the hypotenuse of the right triangle, h. So the magnitude of h is
Plugging in the numbers gives you the following:

Voilà! The bench is only 100 meters away. So instead of walking 80.0 meters east and then 60.0 meters north, a total distance of 140 meters, you only need to walk 100 meters. Your superior knowledge of vectors has saved you 40 meters.
But in what direction is the bench? You know it’s 100 meters away — but 100 meters which way? You find the angle from the x-axis with this trig:
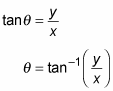
So plugging in the numbers, you have
Therefore, the angle
is the following (using the handy tan–1 button on your calculator):
And there you have it — the nearest bench is 100 meters away at 36.9 degrees from the x-axis. You start off confidently in a straight line at 36.9 degrees from the east, surprising the person who gave you directions, who was expecting you to take off in the goofy zigzag path she’d given you.

