Single-sum problems involve a single amount of money that you either have on hand now or want to have in the future. You use these two tables to figure single sums:
Future value of 1: This table shows how much a single sum on deposit will grow when invested for a specific period of time at a particular interest rate. For example, you deposit $500 in the bank today and want to know how much you’ll have two years from now.
Present value of 1: The flipside of future value, this table tells you how much you’ll have to save today to have a certain amount at your disposal in the future. For example, you want to have $2,000 saved for a down payment on a new car in three years — how much do you need to put away today to reach that goal?
Future value of a single sum
Suppose that a company with an extra $100,000 lying around is trying to decide between investing the money at 4 percent for five years and using the extra money to expand the business. It sure would help if they know how much the $100,000 would grow if they invested it.
Future value table to the rescue! Using this table, the company can calculate exactly what the $100,000 will grow to using the three variables of principal ($100,000), time (five years), and rate (4 percent).
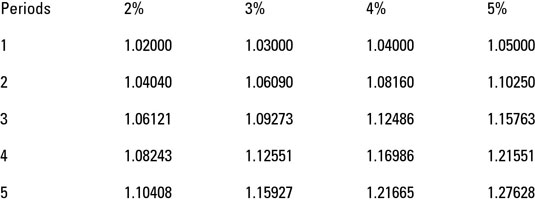
For this calculation, you find the number at the intersection of 4 percent and five periods, which is 1.21665. Multiply $100,000 times 1.21665 to get the future value of a single sum of $100,000. The future value of that single sum is $121,665 ($100,000 x 1.21665).
The company now has valuable information. If it reckons that using the $100,000 to expand the business won’t increase the bottom line over the next five years by at least $21,665 ($121,665 – $100,000), investing the money at 4 percent is probably the wiser option.
Present value of a single sum
Computing the future value of a sum results in a larger amount than what you started with. The opposite is true when figuring the present value of a single dollar amount. In this case, you start with a smaller figure that, through the magic of compound interest, grows into a larger amount.
Say that a company wants to figure out how much it needs to invest today at 5 percent to have $200,000 three years from now. Following is a partial present value of a single sum table.

For this calculation, you find the factor at the intersection of 5 percent and three periods, which is .86384. Multiply $200,000 times .86384 to see how much the company has to invest today to have $200,000 in the future. The answer to that weighty question is $172,768 ($200,000 x .86384).






