If you put a lot of work into rotating an object, the object starts spinning. And when an object is spinning, all its pieces are moving, which tells a physicist that it has kinetic energy. For spinning objects, you have to convert from the linear concept of kinetic energy to the rotational concept of kinetic energy.
You can calculate the kinetic energy of a body in linear motion with the following equation:
where m is the mass of the object and v is the speed. This formula applies to every bit of the object that’s rotating — each bit of mass has this kinetic energy.
To go from the linear version to the rotational version, you have to go from mass to moment of inertia, I, and from linear velocity to angular velocity,
You can tie an object’s tangential speed to its angular speed like this:
the kinetic-energy equation gives you the following:
The equation looks okay so far, but it holds true only for the one single bit of mass under discussion — each other bit of mass may have a different radius, so you’re not finished. You have to sum up the kinetic energy of every bit of mass like this:
You can simplify this equation. Start by noticing that even though each bit of mass may be different and be at a different radius, each bit has the same angular speed (they all turn through the same angle in the same time).
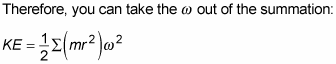
This makes the equation much simpler, because
equals the moment of inertia, I. Making this substitution takes all the dependencies on the individual radius of each bit of mass out of the equation, giving you
Now you have a simplified equation for rotational kinetic energy. The equation proves useful because rotational kinetic energy is everywhere. A satellite spinning around in space has rotational kinetic energy. A barrel of beer rolling down a ramp from a truck has rotational kinetic energy. The latter example (not always with beer trucks, of course) is a common theme in physics problems.

