The most important point elasticity for managerial economics is the point price elasticity of demand. This value is used to calculate marginal revenue, one of the two critical components in profit maximization. (The other critical component is marginal cost.) Profits are always maximized when marginal revenue equals marginal cost.
The formula to determine the point price elasticity of demand is
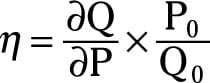
In this formula, ∂Q/∂P is the partial derivative of the quantity demanded taken with respect to the good’s price, P0 is a specific price for the good, and Q0 is the quantity demanded associated with the price P0.
The following equation represents soft drink demand for your company’s vending machines:
In the equation, Q represents the number of soft drinks sold weekly, P is the price per bottle from the vending machine in dollars, I is weekly income in dollars, PC is the price at a convenience in dollars, and A is weekly advertising expenditures in dollars.
Assume initially that P is $1.50, I is $600, PC is $1.25, and A is $400. Substituting those values into the demand equation indicates that 2,000 bottles will be sold weekly.
To determine the point price elasticity of demand given P0 is $1.50 and Q0 is 2,000, you need to take the following steps:
Take the partial derivative of Q with respect to P, ∂Q/∂P.
For your demand equation, this equals –4,000.
Determine P0 divided by Q0.
Because P is $1.50, and Q is 2,000, P0/Q0 equals 0.00075.
Multiply the partial derivative, –4,000, by P0/Q0, 0.00075.
The point price elasticity of demand equals –3.
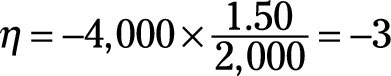
Therefore, at this point on the demand curve, a 1 percent change in price causes a 3 percent change in quantity demanded in the opposite direction (because of the negative sign).
In order to maximize profits, you need to know how much each additional unit you sell adds to your revenue, or in other words, you need to know marginal revenue. If you know the point price elasticity of demand, η, the following formula can enable you to quickly determine marginal revenue, MR, for any given price.
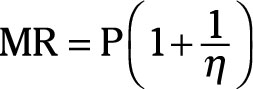
Assume your company charges a $1.50 per bottle of soft drink, and the point price elasticity of demand is –3. To determine how much revenue you add by selling an additional bottle:
Determine (1 + 1/ç).
Substituting –3 for η gives (1 + 1/[–3]) or (1 – 1/3) or 2/3.
Multiply the price, $1.50, by 2/3.
The marginal revenue equals $1.00.
So the marginal revenue received when an additional bottle is sold is
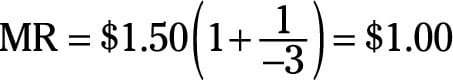
If your cost of providing the extra bottle is less than $1.00, you will increase your profits by selling it.
Similarly, you can calculate point elasticities for the income elasticity of demand, cross-price elasticity of demand, and advertising elasticity of demand using the following formulas:
The point income elasticity of demand:
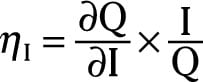
In this formula, ∂Q/∂I is the partial derivative of the quantity taken with respect to income, I is the specific income level, and Q is the quantity purchased at the income level I.
The point cross-price elasticity of demand:
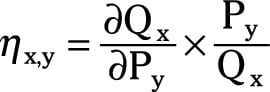
In this formula, ∂Qx/∂Py is the partial derivative of good x’s quantity taken with respect to good y’s price, Py is a specific price for good y, and Qx is the quantity of good x purchased given the price Py.
The point advertising elasticity of demand:
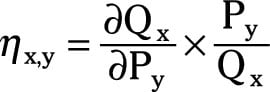
In this formula, ∂Q/∂A is the partial derivative of the quantity demanded taken with respect to advertising expenditures, A is the specific amount spent on advertising, and Q is the quantity purchased.

