In physics, you can calculate power based on force and speed. Because work equals force times distance, you can write the equation for power the following way, assuming that the force acts along the direction of travel:
where s is the distance traveled. However, the object’s speed, v, is just s divided by t, so the equation breaks down to
That’s an interesting result — power equals force times speed? Yep, that’s what it says. However, because you often have to account for acceleration when you apply a force, you usually write the equation in terms of average power and average speed:
Here’s an example. Suppose your brother got himself a snappy new car. You think it’s kind of small, but he claims it has over 100 horsepower. “Okay,” you say, getting out your clipboard. “Let’s put it to the test.”
Your brother’s car has a mass of
On the big Physics Test Track on the edge of town, you measure its acceleration as 4.60 meters/second2 over 5.00 seconds when the car started from rest. How much horsepower is that?
You know that
so all you need to calculate is the average speed and the net applied force. Take the net force first. You know that F = ma, so you can plug in the values to get
Okay, so the force applied to accelerate the car steadily is 5,060 newtons. Now all you need is the average speed. Say the starting speed was vi and the ending speed vf . You know that vi = 0 m/s, so what is vf? Well, you also know that because the acceleration was constant, the following equation is true:
vf = vi + at
As it happens, you know that acceleration and the time the car was accelerated over:
vf = 0 m/s + (4.60 m/s2)(5.00 s) = 23.0 m/s
Because the acceleration was constant, the average speed is
Because vi = 0 m/s, this breaks down to
Plugging in the numbers gives you the average velocity:
Great — now you know the force applied and the average speed. You can use the equation
to find the average power. In particular
You still need to convert to horsepower. One horsepower = 745.7 watts, so
Therefore, the car developed an average of 78.0 horsepower, not 100 horsepower. “Rats,” says your brother. “I demand a recount.”
Okay, so you agree to calculate power another way. You know you can also calculate average power as work divided by time:
And the work done by the car is the difference in the beginning and ending kinetic energies:
W = KEf – KEi
The car started at rest, so KEi = 0 J. That leaves only the final kinetic energy to calculate:
Plugging in the numbers gives you:
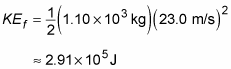
So because
and the work done was
you get the following:
And, as before
“Double rats,” your brother says.






