You can calculate the instantaneous speed of an object using limits. Say that you and your calculus-loving cat are hanging out one day, and you decide to drop a ball out of your second-story window. Here’s the formula that tells you how far the ball has dropped after a given number of seconds (ignoring air resistance):
(where h is the height the ball has fallen, in feet, and t is the amount of time since the ball was dropped, in seconds).
If you plug 1 into t, h is 16; so the ball falls 16 feet during the first second.
Now, what if you wanted to determine the ball’s speed exactly 1 second after you dropped it? You can start by whipping out this trusty ol’ formula:
Using the rate, or speed formula, you can easily figure out the ball’s average speed during the 2nd second of its fall. Because it dropped 16 feet after 1 second and a total of 64 feet after 2 seconds, it fell 64 – 16, or 48 feet, from t = 1 second to t = 2 seconds.
The following formula gives you the average speed:
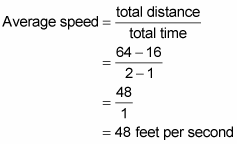
But this isn’t the answer you want because the ball falls faster and faster as it drops, and you want to know its speed exactly 1 second after you drop it. The ball speeds up between 1 and 2 seconds, so this average speed of 48 feet per second during the 2nd second is certain to be faster than the ball’s instantaneous speed at the end of its 1st second.
For a better approximation, calculate the average speed between t = 1 second and t = 1.5 seconds.
Its average speed is thus:

If you continue this process for elapsed times of a quarter of a second, a tenth of a second, then a hundredth, a thousandth, and a ten-thousandth of a second, you arrive at the list of average speeds shown in this table.
| t seconds | 2 | 1 1/2 | 1 1/4 | 1 1/10 | 1 1/100 | 1 1/1,000 | 1 1/10,000 |
| Ave. speed from 1 sec. to t sec. | 48 | 40 | 36 | 33.6 | 32.16 | 32.016 | 32.0016 |
As t gets closer and closer to 1 second, the average speeds appear to get closer and closer to 32 feet per second.
Here’s the formula that you can use to generate the numbers in the table. It gives you the average speed between 1 second and t seconds:
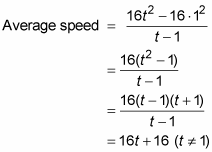
The following figure shows a graph of this equation.
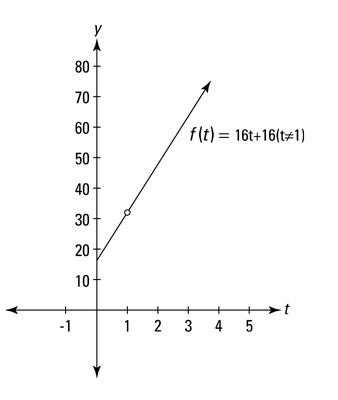
This graph is identical to the graph of the line y = 16t + 16, except for the hole at (1, 32).
There’s a hole because if you plug 1 into t in the average speed function, you get
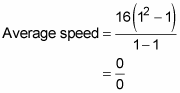
which is undefined. And why did you get 0/0? Because you’re trying to determine an average speed — which equals total distance divided by elapsed time — from t = 1 to t = 1. But from t = 1 to t = 1 is, of course, no time, and “during” this point in time, the ball doesn’t travel any distance, so you get
Obviously there’s a problem here. Hold on to your hat, you’ve arrived at one of the big “Ah ha!” moments in the development of differential calculus.
Instantaneous speed is defined as the limit of the average speed function as the elapsed time approaches zero.
The fact that the elapsed time never gets to zero doesn’t affect the precision of the answer to this limit problem — the answer is exactly 32 feet per second, the height of the hole in the figure. Thirty-two is the answer because as x gets closer and closer to 1, y gets closer and closer to 32. What’s remarkable about limits is that they enable you to calculate the precise, instantaneous speed at a single point in time by taking the limit of a function that’s based on an elapsed time, a period between two points of time.

