In physics, you can apply Newton’s first and second laws to calculate the centripetal acceleration of an orbiting object. Newton’s first law says that when there are no net forces, an object in motion will continue to move uniformly in a straight line. For an object to move in a circle, a force has to cause the change in direction — this force is called the centripetal force. Centripetal force is always directed toward the center of the circle.
The centripetal acceleration is proportional to the centripetal force (obeying Newton’s second law). This is the component of the object’s acceleration in the radial direction (directed toward the center of the circle), and it’s the rate of change in the object’s velocity as the object moves in a circle; the centripetal force does not change the magnitude of the velocity, only the direction.
You can connect angular quantities, such as angular velocity, to centripetal acceleration. Centripetal acceleration is given by the following equation:
where vis the velocity and r is the radius. Linear velocity is easy enough to tie to angular velocity because
Therefore, you can rewrite the acceleration formula as
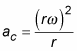
The centripetal-acceleration equation simplifies to
Nothing to it. The equation for centripetal acceleration means that you can find the centripetal acceleration needed to keep an object moving in a circle given the circle’s radius and the object’s angular velocity.
Say that you want to calculate the centripetal acceleration of the moon around the Earth. Start with the old equation
First you have to calculate the tangential velocity of the moon in its orbit. Alternatively, you can use the new version of the equation,
This is easier because the moon orbits the Earth in about 28 days, so you can easily calculate the moon’s angular velocity.
Because the moon makes a complete orbit around the Earth in about 28 days, it travels
around the Earth in that period, so its angular velocity is
Converting 28 days to seconds gives you the following:
Therefore, you get the following angular velocity:
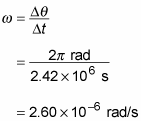
You now have the moon’s angular velocity,
The average radius of the moon’s orbit is
so its centripetal acceleration is
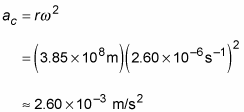
In the preceding equation, the units of angular velocity, radians per second, are written as s–1 because the radian is a dimensionless unit. A radian is the angle swept by an arc that has a length equal to the radius of the circle. Think of it as a particular portion of the whole circle; as such, it has no dimensions. So when you have “radians per second,” you can omit “radians,” which leaves you with “per second.” Another way to write this is to use the exponent –1, so you can represent radians per second as s–1.
Just for kicks, you can also find the force needed to keep the moon going around in its orbit. Force equals mass times acceleration, so you multiply acceleration by the mass of the moon,






