The sum and difference formulas for tangent are very useful if you want to prove some basic trig identities. For example, you can prove the co-function identities by using the difference formula and the periodicity identities by using the sum formula. If you see a sum or a difference inside a tangent function, you can try the appropriate formula to simplify things.
For instance, you can prove this identity,
with the following steps:
Look for identities for which you can substitute.
On the left side of the equal sign, you may use the sum identity for tangent:

Working on the left side only gives you the following equation:

Use any applicable unit circle values to simplify the proof.
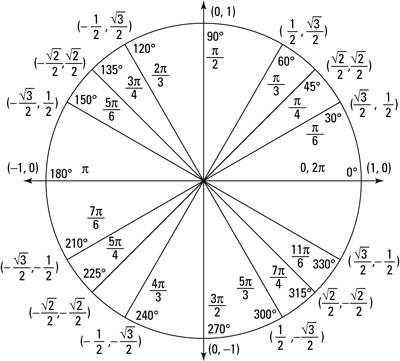 The whole unit circle
The whole unit circleFrom the unit circle, you see that

so you can plug in that value to get this:

From there, simple multiplication gives you the result that proves the equality:







